Cho hàm số $\Large f(x)$ có bảng biến thiên như sau: Số giá trị nguyên

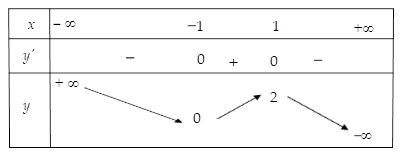
Cho hàm số $\Large f(x)$ có bảng biến thiên như sau:

Số giá trị nguyên của tham số m để phương trình $\Large f(\sin x) = m$ có nghiệm là

• A. A. 1
• B. B. 2
• C. C. 3
• D. D. Vô số

Đặt $\Large t = \sin x$ với $\Large t\in[-1; 1]$ thì phương trình đã cho trở thành $\Large f(x)= m$

Bài toán được thỏa mãn khi đường thẳng y = m có điểm chung với đồ thị hàm số $\Large f(x)$ với hoành độ giao điểm thuộc đoạn [-1; 1]

Dựa vào bảng biến thiên ta suy ra $\Large m \in [0; 2]$

Vì $\Large m \in \mathbb{Z}$ và $\Large m \in [0; 2]$ nên $\Large m \in \left\{0; 1; 2\right\}$

Vậy có tất cả 3 số nguyên m thỏa mãn yêu cầu đề bài