Cho hình nón đỉnh S, đáy là đường tròn tâm O, chiều cao bằng $\Large a

Cho hình nón đỉnh S, đáy là đường tròn tâm O, chiều cao bằng $\Large a\sqrt{3}$. Mặt phẳng (P) đi qua S và cắt đường tròn đáy tại A, B sao cho $\Large \widehat{ASB}=120^{o}$. Biết rằng khoảng cách từ O đến (P) bằng $\Large \dfrac{\a\sqrt{6}}{2}.$ Diện tích xung quanh của hình nón đã cho bằng

• A. $\Large 6\pi a^{2}$
• B. $\Large 4\sqrt{14}\pi a^{2}$
• C. $\Large 12\pi a^{2}$
• D. $\Large 6\sqrt{14}\pi a^{2}$

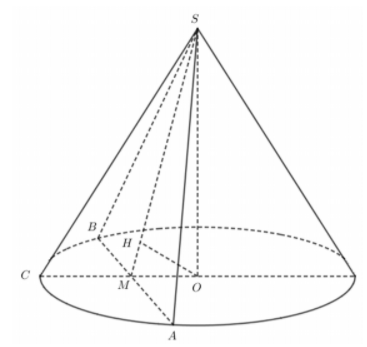Kẻ bán kính OC của (O) vuoonng góc với AB tại M như hình vẽ

Kẻ $\Large OH\perp SM$ tại $\Large H(1)$

Ta có

$\Large AB\perp OC, AB\perp SO$ vì SO vuông góc mặt đáy. Suy ra $\Large AB\perp (SOM)$

Mà $\Large OH\subset (SOM)$. Suy ra $\Large AB\perp OH(2)$

Từ (1) và (2) suy ra $\Large OH\perp (SAB)\Rightarrow d_(O,(P))=OH=\dfrac{a\sqrt{6}}{2}$

Ta có:

$\Large \dfrac{1}{OH^{2}}=\dfrac{1}{SO^{2}}+\dfrac{1}{OM^{2}}\Rightarrow \dfrac{1}{OM^{2}}=\dfrc{1}{OH^{2}}-\dfrac{1}{SO^{2}}=\dfrac{1}{3}\Rightarrow OM=a\sqrt{3}$

$\Large SM=\sqrt{SO^{2}+OM^{2}}=a\sqrt{6},\widehat{ASM}=\dfrac{1}{2}\widehat{ASB}=60^{o}$

$\Large SC=SA=\dfrac{SM}{\cos \widehat{ASM}}=2a\sqrt{6}$

$\Large OC=\sqrt{SC^{2}-SO^{2}}=a\sqrt{21}$

$\Large S_{xq}=\pi.OC.SC=6a\sqrt{14}$