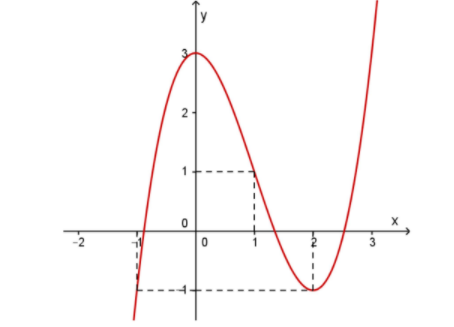
Cho hàm số $\Large y=f(x)=ax^{3}+bx^{2}+cx+d$ có đồ thị như hình vẽ Số

Cho hàm số $\Large y=f(x)=ax^{3}+bx^{2}+cx+d$ có đồ thị như hình vẽ

Số nghiệm thuộc khoảng $\Large \left(-\dfrac{3\pi}{2};3\pi\right)$ của phương trình $\Large f^{2}(\sin x)-5|f(\sin x)|+6=0$

• A. 13
• B. 7
• C. 12
• D. 9

Đặt $\Large t=\sin x$, với $\Large x\in \left(-\dfrac{3\pi}{2};3\pi\right)\Rightarrow t\in [-1;1]$ ta được phương trình:

$\Large f^{2}(t)-5|f(t)|+6=0\Leftrightarrow$ $\Large \left[\begin{align}&|f(t)|=2\\&|f(t)|=3\\\end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align}&f(t)=\pm 2\\&f(t)=\pm 3\\\end{align}\right.$

Xét phương trình $\Large f(t)=-2$ không có nghiệm $\Large t\in[-1;1]$

Xét phương trình $\Large f(t)=2\Leftrightarrow$ $\Large \left[\begin{align}&t=a\in(0;1)\\&t=b\in(-1;0)\\\end{align}\right.$

+) sin x=a cho 4 nghiệm

+) sin x=b cho 5 nghiệm

Xét phương trình $\Large f(t)=-3$ không có nghiệm $\Large t\in[-1;1]$

Xét phương trình $\Large f(t)=3\Leftrightarrow t=0$ phương trình có 4 nghiệm

Vậy phương trình đã cho có 13 nghiệm