Cho khối hộp $\Large ABCD.A'B'C'D'$ có thể tích bằng 12. Gọi $\Large M

Cho khối hộp $\Large ABCD.A'B'C'D'$ có thể tích bằng 12. Gọi $\Large M;N;P$ lần lượt là trung điểm của $\Large AB;A'C';BB'$. Thể tích khối $\Large CMNP$ bằng

• A. $\Large \dfrac{3}{2}$
• B. $\Large \dfrac{5}{4}$
• C. $\Large \dfrac{5}{48}$
• D. $\Large \dfrac{7}{4}$

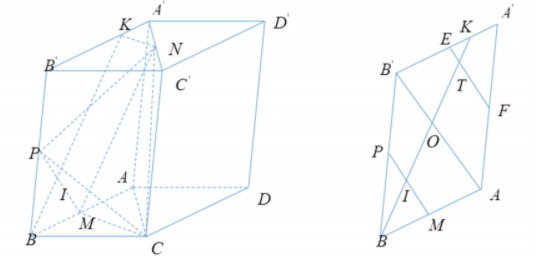Dựng NK song song với $\Large CM, K\in A'B'\Rightarrow NK||(CMP)$. Gọi $\Large I=BK\cap PM$

Ta có $\Large \dfrac{V_{CMNP}}{V_{BPMC}}=\dfrac{d[N,(PMC)]}{d[B,(PMC)]}=\dfrac{d[K,(PMC)]}{d[B,(PMC)]}=\dfrac{KI}{BI}$

Gọi E, F lần lượt là trung điểm của $\Large A'B', A'A;T=BK\cap EF;O=BK\cap AB'$

Ta có $\Large BI=IO=OT=2KT\Rightarrow \dfrac{KI}{BI}=\dfrac{5KT}{2KT}=\dfrac{5}{2}$

Do đó $\Large V_{CMNP}=\dfrac{5}{2}.V_{BPMC}=\dfrac{5}{2}.\dfrac{1}{2}V_{B'BMC}=\dfrac{5}{2}.\dfrac{1}{2}.\dfrac{1}{2}V_{B'ABC}=\dfrac{5}{48}.V_{ACBD.A'B'C'D'}=\dfrac{5}{4}$