Cho hình nón có chiều cao h . Tính chiều cao x của khối trụ có thể tíc

MỤC LỤC
Câu hỏi:
Cho hình nón có chiều cao h. Tính chiều cao x của khối trụ có thể tích lớn nhất nội tiếp trong hình nón theo h.
Đáp án án đúng là: B
Lời giải chi tiết:
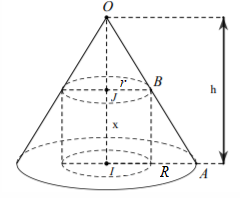
Cho hình nón có chiều cao h. Tính chiều cao x của khối trụ có thể tích lớn nhất nội tiếp trong hình nón theo h.
Gọi R, r theo thứ tự là bán kính đáy hình nón và khối trụ cần tìm. O là đỉnh của hình nón, I là tâm của đáy hình nón, J là tâm của đáy hình trụ và khác I. OA là một đường sinh của hình nón, B là điểm chung của OA với khối trụ.
Ta có: $\large \dfrac{r}{R} = \dfrac{h-x}{h}\Rightarrow r = \dfrac{R}{h}(h-x)$
Thể tích khối trụ là: $\large V = \pi xr^{2} = \pi x\dfrac{R^{2}}{h^{2}}(h-x)^{2}$
Xét hàm số $\large V(x) = \pi x\dfrac{R^{2}}{h^{2}}(h-x)^{2}$, 0
Ta có $\large V'(x) = \pi \dfrac{R^{2}}{h^{2}}(h-x)(h-3x) = 0 \Leftrightarrow x = \dfrac{h}{3}$
Bảng biến thiên:
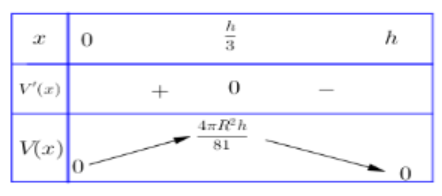
Dựa vào BBT, ta thấy thể tích khối trụ lớn nhất khi chiều cao của khối trụ là $\large x = \dfrac{h}{3}$.
Xem thêm các bài tiếp theo bên dưới
- Trong số các hình trụ có diện tích toàn phần đều bằng S thì bán kính R
- Cho hình chóp S.ABCD có ABCD là hình chữ nhật tâm I cạnh AB = 3a, BC =
- Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm của AB, M, N lần lượt
- Cho hai mặt phẳng ( P ) và ( Q ) song song với nhau và cắt một mặt cầu
- Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a . C