Cho hình chóp S.ABCD có ABCD là hình chữ nhật tâm I cạnh AB = 3a, BC =

Cho hình chóp S.ABCD có ABCD là hình chữ nhật tâm I cạnh AB = 3a, BC = 4a. Hình chiếu của S trên mặt phẳng (ABCD) là trung điểm của ID. Biết rằng SB tạo với mặt phẳng (ABCD) một góc $\large 45^{\circ}$. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD.

• A.

  A. $\large \dfrac{25\pi }{2}a^{2}$

• B.

  B. $\large \dfrac{125\pi }{4}a^{2}$

• C.

  C. $\large \dfrac{125\pi }{2}a^{2}$

• D.

  D. $\large 4\pi a^{2}$

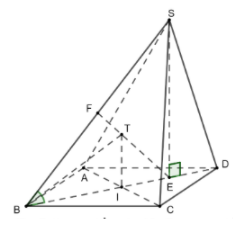
Gọi E là trung điểm của ID, F là trung điểm của SB. Trong mặt phẳng (SBD) vẽ IT song song với SE và cắt EF tại T.

Ta có $\large SE \perp (ABCD)$, suy ra $\large \widehat{SBE} = (SB;(ABCD)) = 45^{\circ}$. Suy ra $\large \Delta SBE$ vuông cân tại E. Suy ra EF là trung trực của SB. Suy ra TS = TB.   (1)

Ta có IT // SE, suy ra $\large IT \perp (ABCD)$. Suy ra IT là trục đường tròn ngoại tiếp hình chữ nhật ABCD. Suy ra TA = TB = TC = TD.    (2)

Từ (1) và (2) suy ra T là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.

Do ABCD là hình chữ nhật nên $\large BD = AC = \sqrt{AB^{2}+BC^{2}} = 5a$, 

suy ra $\large IB = ID = \dfrac{5}{2}a$ 

Do E là trung điểm của ID nên $\large IE = \dfrac{1}{2}ID = \dfrac{5}{4}a$ 

$\large \Delta BEF$ vuông tại F có $\large \widehat{EBF} = 45^{\circ}$ nên $\large \Delta BEF$ vuông cân tại F.

$\large \Delta EIT$ vuông tại I có $\large \widehat{IET} = 45^{\circ}$ nên $\large \Delta EIT$ vuông cân tại I.

Suy ra $\large IT = IE = \dfrac{5}{4}a$.

Do $\large \Delta BIT$ vuông tại I nên $\large TB = \sqrt{IB^{2}+IT^{2}} = \dfrac{5\sqrt{5}}{4}a$ 

Vậy diện tích mặt cầu ngoại tiếp hình chóp S.ABCD là 

$\large S = 4\pi TB^{2} = \dfrac{125\pi }{4}a^{2}$.