Cho hình nón có bán kính đáy là 5 a , độ dài đường sinh là 13 a . Thể

Cho hình nón có bán kính đáy là 5a, độ dài đường sinh là 13a. Thể tích khối cầu nội tiếp hình nón bằng:

• A.

  A. $\large \dfrac{4000\pi a^{3}}{81}$

• B.

  B. $\large \dfrac{4000\pi a^{3}}{27}$

• C.

  C. $\large \dfrac{40\pi a^{3}}{9}$

• D.

  D. $\large \dfrac{400\pi a^{3}}{27}$

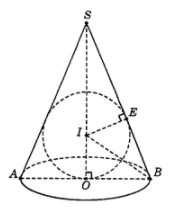
Xét mặt phẳng qua trục SO của hình nón ta được thiết diện là tam giác cân SAB.

Mặt phẳng đó cắt mặt cầu theo đường tròn có bán kính r (bán kính mặt cầu) và nội tiếp trong tam giác cân SAB.

Trong tam giác vuông SOB, gọi I là giao điểm của đường phân giác trong góc B với đường thẳng SO.

Chứng minh được I là tâm đường tròn nội tiếp tam giác và bán kính r = IO = IE (E là hình chiếu vuông góc của I trên SB).

Theo tính chất phân giác, ta có $\large \dfrac{IS}{IO} = \dfrac{BS}{BO} = \dfrac{13}{5}$.

Lại có $\large IS+IO = SO = \sqrt{SB^{2}-OB^{2}} = 12a$.

Từ đó suy ra $\large IS = \dfrac{26}{3}a, IO = \dfrac{10}{3}a$.

Ta có $\large \Delta SEI \sim \Delta SOB$ nên

$\large \dfrac{IE}{IS} = \dfrac{BO}{BS} = \dfrac{5}{13}\Rightarrow IE = \dfrac{5}{13}IS = \dfrac{10}{3}a$ 

Thể tích khối cầu:

$\large V = \dfrac{4}{3}\pi r^{3} = \dfrac{4}{3}\pi \left (\dfrac{10a}{3}  \right )^{3} = \dfrac{4000\pi a^{3}}{81}$ (đvtt). Chọn A.