Cho hình trụ có bán kính bằng r và chiều cao cũng bằng r. Một hình vuô

Cho hình trụ có bán kính bằng r và chiều cao cũng bằng r. Một hình vuông ABCD có hai cạnh AB,CD lần lượt là các dây cung của hai đường tròn đáy, còn cạnh BC, AD không phải là đường sinh của hình trụ. Tan của góc giữa mặt phẳng chứa hình vuông và mặt đáy bằng:

• A.

  A. 1

• B.

  B. $\large \dfrac{\sqrt{6}}{2}$

• C.

  C. $\large \dfrac{\sqrt{6}}{3}$

• D.

  D. $\large \dfrac{\sqrt{15}}{5}$

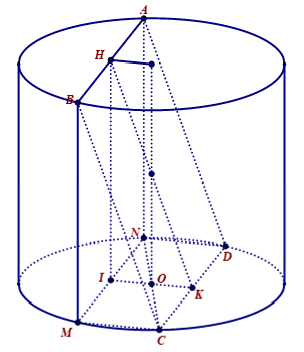
Chọn C

Gọi MN là hình chiếu vuông góc của AB lên đường tròn đáy. Ta có MNDC là hình chữ nhật và $\large NC \cap MD = O$ là tâm đường tròn đáy. Gọi H, I, K lần lượt là trung điểm AB, MN, CD. 

Lại có $\large HK \perp CD, IK \perp CD$, suy ra góc giữa mặt phẳng chứa hình vuông ABCD và mặt đáy là

$\large \widehat{HKI} \Rightarrow tan\widehat{HKI} = \dfrac{IH}{IK}$.

Đặt AB = BC = CD = AD = x (x>0). Ta có

$\large MC = IK = 2OK = 2\sqrt{OC^{2}-CK^{2}} = 2\sqrt{r^{2}-\dfrac{x^{2}}{4}}$ 

Trong tam giác vuông BMC ta có

$\large BM^{2}+MC^{2} = BC^{2}\Leftrightarrow r^{2}+4\left (r^{2}-\dfrac{x^{2}}{4}  \right ) = x^{2}$ 

$\large \Leftrightarrow x = \dfrac{r\sqrt{5}}{\sqrt{2}}\Rightarrow IK = \dfrac{r\sqrt{3}}{\sqrt{2}}$ 

Suy ra:

$\large tan\widehat{HKI} = \dfrac{IH}{IK} = \dfrac{r}{\dfrac{r\sqrt{3}}{\sqrt{2}}} = \dfrac{\sqrt{2}}{\sqrt{3}} = \dfrac{\sqrt{6}}{3}$