Cho hình nón đỉnh S , đáy là hình tròn tâm O , góc ở đỉnh bằng $\large

Cho hình nón đỉnh S, đáy là hình tròn tâm O, góc ở đỉnh bằng $\large 120^{\circ}$. Trên đường tròn đáy, lấy điểm A cố định và điểm M di động. Có bao nhiêu vị trí điểm của điểm M để diện tích tam giác SAM đạt giá trị lớn nhất?

• A. A. 2
• B. B. 3
• C. C. 1
• D. D. vô số

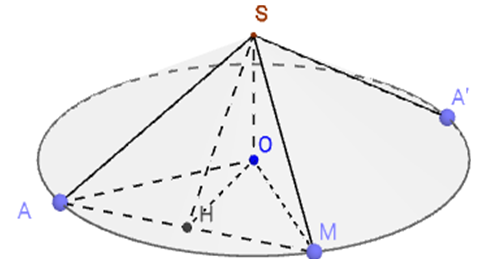
Chọn A

Gọi r là bán kính đáy của hình nón.

Vì góc ở đỉnh $\large \widehat{ASA'} = 120^{\circ} \Rightarrow \widehat{ASO} = 60^{\circ}$. 

Suy ra $\large SO = OA.cot\widehat{ASO} = \dfrac{r}{\sqrt{3}}$.

Gọi H là trung điểm của AM và đặt x = OH.

Ta có: $\large SH = \sqrt{SO^{2}+OH^{2}} = \sqrt{\dfrac{r^{2}}{3}+x^{2}}$,

$\large AM = 2AH = 2\sqrt{OA^{2}-OH^{2}} = 2\sqrt{r^{2}-x^{2}}$.

Diện tích tam giác $\large \Delta$SAM bằng 

$\large S_{SAM} = \dfrac{1}{2}SH.AM =  \sqrt{\dfrac{r^{2}}{3}+x^{2}}.\sqrt{r^{2}-x^{2}}\leq \dfrac{2}{3}r^{2}$ 

$\large S_{SAM max} = \dfrac{2}{3}r^{2}$ đạt được khi 

$\large \dfrac{r^{2}}{3}+x^{2} = r^{2}-x^{2} \Leftrightarrow x^{2} = \dfrac{r^{2}}{3}\Leftrightarrow x = \dfrac{r}{\sqrt{3}}$ 

Tức là OH = SO.

Theo tính chất đối xứng của đường tròn ta có hai vị trí của M thỏa mãn yêu cầu.