Có một miếng bìa hình chữ nhật ABCD với AB = 3 và AD = 6. Trên cạnh AD

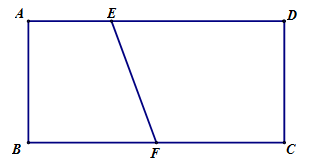
Có một miếng bìa hình chữ nhật ABCD với AB = 3 và AD = 6. Trên cạnh AD lấy điểm E sao cho AE = 2, trên cạnh BC lấy điểm F là trung điểm của BC. Cuốn miếng bìa lại sao cho AB và DC trùng nhau để tạo thành mặt xung quanh của một hình trụ. Khi đó thể tích V của tứ diện ABEF.

• A.

  A. $\large V= \dfrac{\pi }{3}$

• B.

  B. $\large V= \dfrac{9\sqrt{3}}{2\pi ^{2}}$

• C.

  C. $\large V= \dfrac{3\pi ^{3}}{2}$

• D.

  D. $\large V= \dfrac{2}{3\pi ^{2}}$

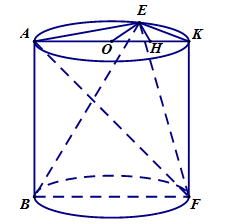
Từ giả thiết suy ra BF là đường kính đường tròn đáy của hình trụ.

Kẻ đường sinh FK, gọi O là trung điểm AK.

Gọi r là bán kính đáy, suy ra $\large 2\pi r = 6\Leftrightarrow r = \dfrac{3}{\pi }$.

Đặt $\large \widehat{AOE} = \alpha$ (rad). Trong hình chữ nhật ABCD có AE = 2

$\large \Rightarrow l_{\widehat{AOE}} = r.\alpha \Rightarrow \widehat{AOE} = \alpha = \dfrac{2}{r } = \dfrac{2\pi }{3}\Rightarrow \widehat{EOK} = \dfrac{\pi }{3}$,

suy ra tam giác EOK là tam giác đều cạnh $\large r = \dfrac{3}{\pi }$.

Gọi H là trung điểm OK $\large \Rightarrow EH \perp AK, EH \perp AB$ 

$\large \Rightarrow EH \perp (ABFK)\Rightarrow d(E,(ABF)) = EH = \dfrac{r\sqrt{3}}{2} = \dfrac{3\sqrt{3}}{2\pi }$ 

Diện tích tam giác ABF là 

$\large S = \dfrac{1}{2}.AB.BF = \dfrac{1}{2}.3.\dfrac{6}{\pi } = \dfrac{9}{\pi }$ 

Thể tích khối tứ diện ABEF là 

$\large V = \dfrac{1}{3}S_{ABF}.d(E,(ABF)) = \dfrac{1}{3}.\dfrac{9}{\pi }.\dfrac{3\sqrt{3}}{2\pi } = \dfrac{9\sqrt{3}}{2\pi ^{2}}$