Cho một khối trụ có bán kính đáy r = a và chiều cao h = 2a . Mặt phẳng
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho một khối trụ có bán kính đáy r = a và chiều cao h = 2a. Mặt phẳng (P) song song với trục OO’ của khối trụ chia khối trụ thành 2 phần, gọi V1 là thể tích phần khối trụ chứa trục OO’, V1 là thể tích phần còn lại của khối trụ. Tính tỉ số V1V2, biết rằng (P) cách OO’ một khoảng bằng a√22.
Đáp án án đúng là: A
Lời giải chi tiết:
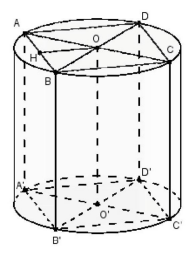
Thể tích khối trụ V=πr2h=πa2.2a=2πa3.
Gọi thiết diện là hình chữ nhật ABB’A’.
Dựng lăng trụ ABCD.A’B’C’D’ như hình vẽ.
Gọi H là trung điểm AB.
Ta có OH⊥AB⇒OH⊥(ABB′A′)⇒OH=a√22
⇒AH=BH=a√22=OH
⇒ΔOAB vuông cân tại O ⇒ ABCD là hình vuông.
Từ đó suy ra:
V2=14(V−VABCD.A′B′C′D′)=14(2πa3−(a√2)2.2a)=a3(π−2)2
V1=V−V2=2πa3−a3(π−2)2=a3(3π+2)2
Suy ra V1V2=3π+2π−2
Chọn A.
Xem thêm các bài tiếp theo bên dưới
- Có một miếng bìa hình chữ nhật ABCD với AB = 3 và AD = 6. Trên cạnh AD
- Cho hình trụ có bán kính bằng r và chiều cao cũng bằng r. Một hình vuô
- Tripeptit là hợp chất A. có liên kết peptit mà phân tử có 3 gốc amino
- Amino axit là hợp chất hữu cơ trong phân tử A. chứa nhóm cacboxyl và n
- Amin có cấu tạo $\Large \mathrm {CH}_{3} \mathrm {CH}_{2} \mathrm {CH(