Một hình thang cân có chiều cao h và độ dài hai đáy là a, b . Tính thể

Một hình thang cân có chiều cao h và độ dài hai đáy là a, b. Tính thể tích vật thể tròn xoay thu được khi quay hình thang này quanh đường trung trực của hai đáy

• A.

  A. $\large \dfrac{1}{3}\pi h(a^{2}+ab+b^{2})$

• B.

  B. $\large \dfrac{1}{6}\pi h(a^{2}+ab+b^{2})$

• C.

  C. $\large \dfrac{1}{12}\pi h(a^{2}+ab+b^{2})$

• D.

  D. Cả A, B, C đều sai

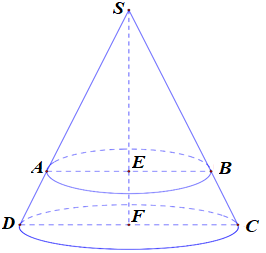
Chọn C

Gọi E, F lần lượt là trung điểm của AB, CD.

Theo giả thiết, ta có $\large EB = \dfrac{a}{2}, FC = \dfrac{b}{2}$ và EF = h. Đặt SE = x.

$\large \Delta SEB \sim \Delta SFC \Rightarrow \dfrac{SE}{SF} = \dfrac{EB}{FC}\Rightarrow \dfrac{x}{x+h} = \dfrac{a}{b}\Rightarrow x = \dfrac{ah}{b-a}$ 

Suy ra $\large SF = \dfrac{ah}{b-a} + h = \dfrac{bh}{b-a}$ 

Thể tích vật tròn xoay cần tìm là:

$\large V = \dfrac{1}{3}\pi .SF.FC^{2}-\dfrac{1}{3}\pi .SE.EB^{2} = \dfrac{1}{3}\pi .\left (\dfrac{bh}{b-a}.\dfrac{b^{2}}{4}-\dfrac{ah}{b-a}.\dfrac{a^{2}}{4}  \right )$ 

$\large = \dfrac{1}{3}\pi .\dfrac{h}{4(b-a)}.(b^{3}-a^{3}) = \dfrac{1}{12}\pi h.(a^{2}+ab+b^{2})$.