Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Số đo góc giữa hai m

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Số đo góc giữa hai mặt phẳng (BA’C’) và (DA’C) bằng 

• A. A. $\large 60^\circ $
• B. B. $\large 90^\circ $
• C. C. $\large 120^\circ $
• D. D. $\large 30^\circ $

Chọn A

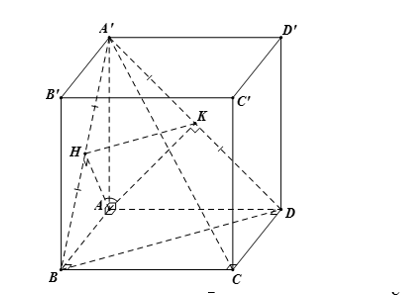
ta có: $\large AH\perp (BA’C),\, AK\perp (SA’C)$ với H, K lần lượt là trung điểm của A’B, A’D
Suy ra: $\large \angle ((BA’C), (DA’C))= \angle (AH, AK) = \angle HAK$
Lại có: HK là trung trung bình của $\large \Delta A’BD$ nên $\large HK = \dfrac{1}{2}BD= \dfrac{a\sqrt{2}}{2}$
Mặt khác: $\large AH= AK= \dfrac{a\sqrt{2}}{2}$
Do đó: $\large AH= AK= HK= a\sqrt{2}$
Suy ra: $\large \Delta AHK$ đề
Vậy $\large \angle ((BA’C), (DA’C))= \angle HAK= 60^\circ $