Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng 1 và các góc ph

Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng $\large 60^\circ $. Tính khoảng cách giữa hai đường thẳng AB’ và A’C’

• A. A. $\large \dfrac{\sqrt{22}}{11}$
• B. B. $\large \dfrac{2}{11}$
• C. C. $\large \dfrac{\sqrt{2}}{11}$
• D. D. $\large \dfrac{3}{11}$

ChọnA

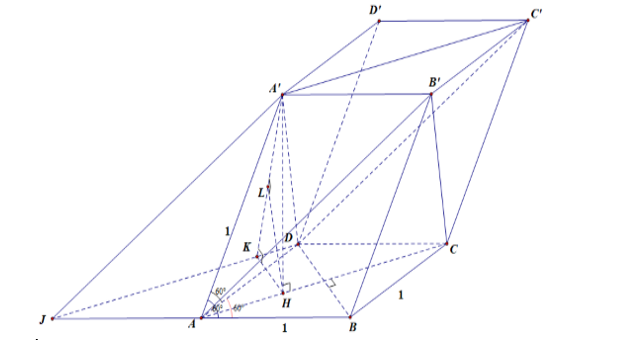
Ta có: $\large \widehat{BAA’}= \widehat{DAA}= \widehat{BAD}= 60^\circ $ và $\large AB=AD= AA’= 1$ 
Khi đó: $\large de ABD,\, \Delta ADA’,\, \Delta ABA]$ đều cạnh bằng 1
$\large \Rightarrow  A’D= A’A= A’B= 1$. Suy ra hình chiếu của A’ lên (ABCD) là tâm H của $\large \Delta ABD$ đều 
Ta có: $\large AB’// DC’\Rightarrow  d(AB’, A’C’)= d(AB’, (DA’C’))= d(H, (DA’C’))$
Dựng hình bình hành DCAJ. Từ H kẻ $\large HK\perp DJ,\, (K\in DJ)$, ta có: $\large HK//BD$
Từ H kẻ $\large HL\perp A’K,\, (L\in A’K)\Rightarrow  HL\perp (SA’C’)\Rightarrow  d(H, (DA’C’))= HL$ 
Ta có: $\large HK= \dfrac{1}{2}A’H= \sqrt{1-\left( \dfrac{\sqrt{3}}{3}\right)^2}= \dfrac{\sqrt{6}}{3}$
Xét tam giác $\large A’HK:\, \dfrac{1}{HL^2}= \dfrac{1}{HK^2}+ \dfrac{1}{A’H^2}\Rightarrow  HL= \dfrac{\sqrt{22}}{11}$