Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vu

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, cạnh bên SB tạo với đáy góc $\large 45^\circ $. Một mặt phẳng ($\large \alpha $) đi qua A và vuông góc với SC cắt hình chóp S.ABCD theo thiết diện tứ giác AB’C’D’ có diện tích bằng 

• A. A. $\large \dfrac{a^2\sqrt{3}}{4}$
• B. B. $\large \dfrac{a^2\sqrt{3}}{2}$
• C. C. $\large \dfrac{a^2\sqrt{3}}{6}$
• D. D. $\large \dfrac{a^2\sqrt{3}}{3}$

Chọn C

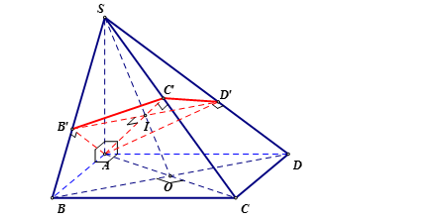
Dễ thấy $\large \widehat{SBA}= 45^\circ $. Ta có: $\large B’D’\perp SC$ và $\large BD\perp SC$ và SC không vuông góc với mặt phẳng (SBD), suy ra $\large BD//B’D’$
Từ trên suy ra $\large B’D’\perp AC’$ và $\large \left\{\begin{align}& AB’\perp SC\\& AB’\perp BC\\\end{align} \right.$ $\large \Rightarrow  AB’\perp SB$
Suy ra: $\large S_{AB’C’D’}= \dfrac{1}{2}AC’.B’D’$ mà $\large AC’=\dfrac{a\sqrt{6}}{3}$ và $\large \dfrac{B’D’}{BD}= \dfrac{SB’}{SB}= \dfrac{a\sqrt{2}}{2.a\sqrt{2}}= \dfrac{1}{2}$
$\large \Rightarrow  B’D’= \dfrac{a\sqrt{2}}{2}$
Vậy $\large S_{AB’C’D’}= \dfrac{1}{2}.AC’.B’D’= \dfrac{a^2\sqrt{3}}{6}$