Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, $\la

Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, $\large AB= AD= 2a,\, DC= a$. Điểm I là trung điểm của AD, mặt phẳng (SIB) và (SIC) cùng vuông góc với mặt phẳng (ABCD). Mặt phẳng (SBC) tạo với mặt phẳng (ABCD) một góc $\large 60^\circ $, tính khoảng cách từ D đến (SBC) theo a

• A. A. $\large \dfrac{2a\sqrt{15}}{5}$
• B. B. $\large \dfrac{9a\sqrt{15}}{10}$
• C. C. $\large \dfrac{9a\sqrt{15}}{20}$
• D. D. $\large \dfrac{a\sqrt{15}}{5}$

Chọn D

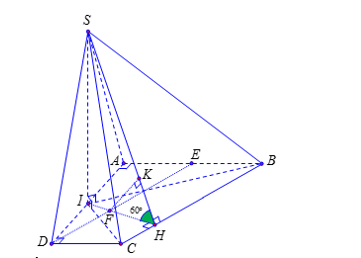
Ta có: $\large \left\{\begin{align}& (SIB)\perp (ABCD)\\& (SIC)\perp (ABCD)\\& (SIB)\perp (SIC)= SI\\\end{align} \right.$ $\large \Rightarrow  SI\perp (ABCD)$
Trong mặt phẳng (ABCD), kẻ $\large IH\perp BC$ thì $\large BC\perp (SIH)\Rightarrow  \angle ((SBC), (ABCD))= \angle SHI$
Mặt khác:
$\large S_{IBC}= S_{ABCD}-S_{ICD}- S_{IAB}$
$\large \Leftrightarrow S_{IBC}= \dfrac{1}{2}AD(AB+CD)- \dfrac{1}{2}{ID.DC}- \dfrac{1}{2}IA.IB\Leftrightarrow S_{IBC}= \dfrac{3a^2}{2}$
Lại có: $\large S_{IBC}= \dfrac{1}{2}IH.BC\Rightarrow  IH=\dfrac{2S_{IBC}}{BC}\Leftrightarrow IH= \dfrac{2S_{IBC}}{\sqrt{AB^2+ DE^2}}\Leftrightarrow IH= \dfrac{3a}{\sqrt{5}}$
Tam giác SIH vuông tại I có $\large SI= IH.tan 60^\circ = \dfrac{3a\sqrt{3}}{\sqrt{5}},\, SH= \dfrac{6a}{\sqrt{5}}$
Gọi E là trung điểm cạnh AB và F là giao điểm của DF và IH
Vì BCDF là hình bình hành nên $\large DF//BC\Rightarrow  d(D, (SBC))= d(F, (SBC))= KF$
Hai tam giác DFI và DAE đồng dạng nên $\large IF= \dfrac{DI.AE}{DE}= \dfrac{a}{\sqrt{5}}\Rightarrow  FH= \dfrac{2a}{\sqrt{5}}$
Hai tam giác HKF và HIS đồng dạng nên $\large KF= \dfrac{SI.HF}{SH}= \dfrac{a\sqrt{15}}{5}$
Vậy $\large d(D, (SBC))= \dfrac{a\sqrt{15}}{5}$