Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khi đó khoảng cách g

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khi đó khoảng cách giữa đường thẳng BD và mặt phẳng (CB’D’) bằng

• A. A. $\large \dfrac{a\sqrt{2}}{2}$
• B. B. $\large \dfrac{2a\sqrt{3}}{3}$
• C. C. $\large \dfrac{a\sqrt{3}}{3}$
• D. D. $\large \dfrac{a\sqrt{6}}{3}$

Chọn C

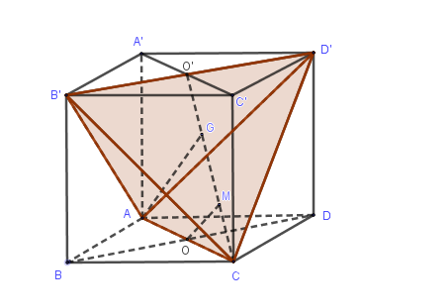
Gọi O, O’ lần lượt là tâm hai đáy ABCD.A’B’C’D’
Vì $\large BD//B’D’$ nên $\large BD// (CB’D’)$
Do đó: $\large d(BD, (CB’D’))= d(O, (CB’D”))= \dfrac{1}{2}d(A, (CB’D’))$
Mà $\large AO\cap (CB’D’)= C\Rightarrow  d(O, (CB’D’))= \dfrac{1}{2}d(A, (CB’D’))$
Vậy $\large d(BD, (CB’D’))= \dfrac{1}{2}d(A, (CB’D’))$
Ta tính $\large d(A, (CB’D’))$
Xét tứ diện ACB’D’ có $\large AB’=AC= AD’= B’C= B’D’= CD’= a\sqrt{2}$ nên nó là tứ giác đều cạnh $\large a\sqrt{2}$
Gọi G là trọng tâm tam giác CB’D’ thì $\large CG= \dfrac{2}{3}CO’= \dfrac{2}{3}.\dfrac{a\sqrt{2}.\sqrt{3}}{2}= \dfrac{a\sqrt{6}}{3}$
Do đó: $\large d(A, CB’D’))= AG= \sqrt{AC^2- CG^2}= \sqrt{2a^2- \dfrac{6a^2}{9}}= \dfrac{2a\sqrt{3}}{3}$
Vậy $\large d(BD, (CB’D’))= \dfrac{1}{2}d(A, (CB’D’))= \dfrac{a\sqrt{3}}{3}$