Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Gọi K là điểm trên cạnh C
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Gọi K là điểm trên cạnh CC' sao cho CK=23a. Mặt phẳng (α) đi qua hai điểm A, K song song với BD, mặt phẳng (α) cắt BB', DD' lần lượt tại M và N. Thể tích của khối đa diện BCDNMK bằng
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
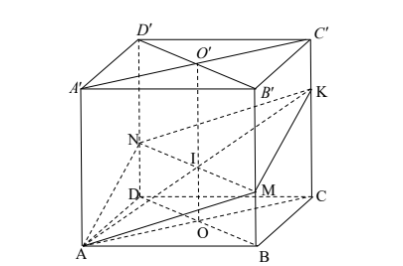
Vì (α)//BD nên MN//BD
Gọi O, O' lần lượt là tâm của hai hình vuông ABCD và A'B'C'D', I=MN∩OO′
⇒BM=IO=12CK=a3
Gọi V là thể tích khối đa diện cần tính
ta có: V=2VOBC.IMK=2(VA.BCKM−VA.OBMI)=2(13.AB.SBCKM−13.OA.SOBMI)=23(AB.SBCKM−OA.SOBMI)
=23[AB.12.BC.(BM+CK)−OA.OB.BM]=23[a.12.a(a3+2a3)−a√22.a√22.a3]=2a39
Xem thêm các bài tiếp theo bên dưới