Cho hàm số y=f(x)y=f(x) có đồ thị như hình vẽ sau: Số nghiệm thuộ
Lưu về Facebook:
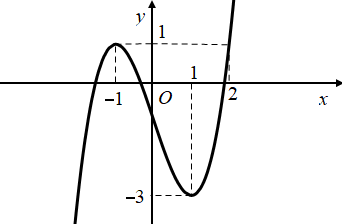
MỤC LỤC
Câu hỏi:
Cho hàm số y=f(x)y=f(x) có đồ thị như hình vẽ sau:
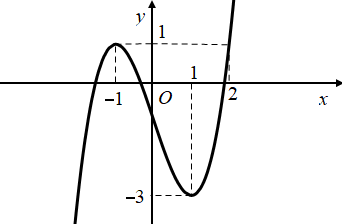
Số nghiệm thuộc đoạn [−π2;3π][−π2;3π] của phương trình 2f(2cosx+1)+3=02f(2cosx+1)+3=0 là:
Đáp án án đúng là: A
Lời giải chi tiết:
Chọn A
Ta có: 2f(2cosx+1)+3=0⇔f(2cosx+1)=−322f(2cosx+1)+3=0⇔f(2cosx+1)=−32
Dựa vào BBT ta có:
f(2cosx+1)=−32<−1⇔f(2cosx+1)=−32<−1⇔ [2cosx+1=m∈(−∞;−2)(1)2cosx+1=m∈(0;1)(2)2cosx+1=p∈(1;2)(3)
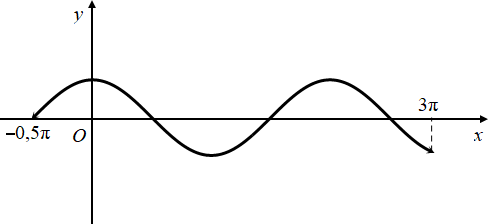
Dựa vào đồ thị hàm số y=cosx trên đoạn [−π2;3π] ta có:
(1)⇔2cosx+1=m∈(−∞;−2)⇔cosx=m−12∈(−∞;−32)⇒ Phương trình vô nghiệm
(2)⇔2cosx+1=n∈(0;1)⇔cosx=n−12∈(−12;0)⇒ phương trình có 3 nghiệm phân biệt
(3)⇔2cosx+1=p∈(1;2)⇔cosx=p−12∈(0;12)⇒ phương trình có 4 nghiệm phân biệt
Xem thêm các bài tiếp theo bên dưới