Cho hình lăng trụ tam giác đều ABC.A’B’C’ có $\large AB=2\sqrt{3}$ và

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có $\large AB=2\sqrt{3}$ và $\large AA’= 2$. Gọi M, N, P lần lượt là trung điểm các cạnh A’B’, A’C’ và BC (tham khảo hình vẽ bên dưới). $\large $ của góc tạo bởi mặt phẳng (AB’C’) và (MNP) bằng 

• A. $\large \dfrac{6\sqrt{13}}{65}$
• B. $\large \dfrac{\sqrt{13}}{65}$
• C. $\large \dfrac{17\sqrt{13}}{65}$
• D. $\large \dfrac{18\sqrt{13}}{65}$

Chọn B

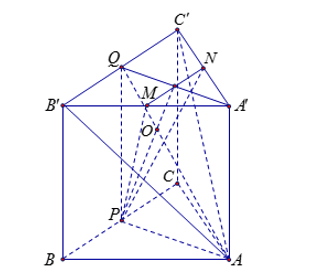
Gọi I, Q lần lượt là trung điểm của MN, B’C’. Gọi $\large O= PI\cap AQ$
Khi đó: $\large \left\{\begin{align}& O\in (AB’C’)\cap (MNP)\\& B’C’//MN\\& B’C’\subset (AB’C’),\, MN\subset (MNP)\\\end{align} \right.$ nên giao tuyến của (AB’C’) và (MNP) là đường thẳng d qua O và song song với MN, B’C’
Tam giác AB’C’ cân tại A nên $\large AQ\perp B’C’\Rightarrow  AQ\perp d$
Tam giác MNP cân tại P nên $\large PI\perp MN\Rightarrow  PI\perp d$
Do đó góc tạo bởi hai mặt phẳng (AB’C’) và (MNP) là góc giữa AQ và PI
Ta có: $\large AP=3,\, AQ= \sqrt{13},\, IP= \dfrac{5}{2}$
Vì $\large \dfrac{AP}{IQ}= 2$ nên $\large OA= \dfrac{2}{3}AQ= \dfrac{2\sqrt{13}}{3};\, OP= \dfrac{2}{3}IP= \dfrac{5}{3}$
$\large \cos\angle ((AB’C’), (MNP))= \cos\angle (AQ, PI)= \left| \cos\angle AOP\right|= \dfrac{OA^2+OP^2-AP^2}{2.OA.OP}= \dfrac{\sqrt{13}}{65}$