Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vu

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy và có đọ dài bằng $\large a\sqrt{2}$. Gọi $\large \alpha $ là góc giữa hai mặt phẳng (SAD) và (SBD). Tính $\large \cos\alpha $

• A. $\large \cos\alpha=\dfrac{3}{5}$
• B. $\large \cos\alpha= \dfrac{\sqrt{6}}{3}$
• C. $\large \cos\alpha= \dfrac{2a\sqrt{2}}{5}$
• D. $\large \cos \alpha= \dfrac{\sqrt{10}}{5}$

Chọn D

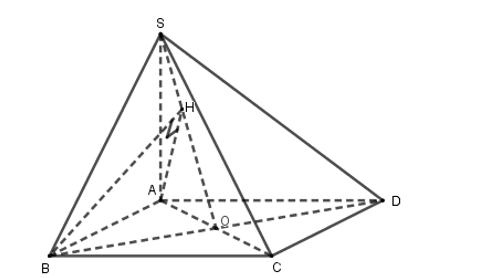
Gọi O là tâm hình vuông ABCD. Kẻ $\large AH\perp SO$ tại H
Ta có: $\large BD\perp AO,\, BD\perp SA\Rightarrow  BD\perp (SAO)\Rightarrow  BD\perp AH$. Vậy $\large AH\perp (SBD)$
Lại có: $\large AB\perp (SAD)$, do đó góc $\large $ giữa hai mặt phẳng (SAD) và (SBD) là góc giữa hai đường thẳng AH và AB. Do đó: $\large \alpha=\widehat{BAH}$ và $\large \widehat{BAH} < 90^\circ = \widehat{BHA}$
Tam giác SAO vuông tại A, đường cao AH nên 
$\large \dfrac{1}{AH^2}= \dfrac{1}{AS^2}+ \dfrac{1}{AO^2}= \dfrac{1}{2a^2}+\dfrac{4}{2a^2}= \dfrac{5}{2a^2}$
Suy ra: $\large AH= \dfrac{a\sqrt{10}}{5}$. Từ đó: $\large \cos\alpha=\dfrac{AH}{AB}= \dfrac{\sqrt{10}}{5}$