Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, P là trung

Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, P là trung điểm của các cạnh SA và SC. Điểm N thuộc cạnh SB sao cho $\large \dfrac{SN}{SB}= \dfrac{2}{3}$. Gọi Q là giao điểm của các cạnh SD và mặt phẳng (MNP). Tính tỉ số $\large \dfrac{SQ}{SD}$

• A. $\large \dfrac{2}{5}$
• B. $\large \dfrac{1}{3}$
• C. $\large \dfrac{3}{8}$
• D. $\large \dfrac{2}{3}$

Chọn A

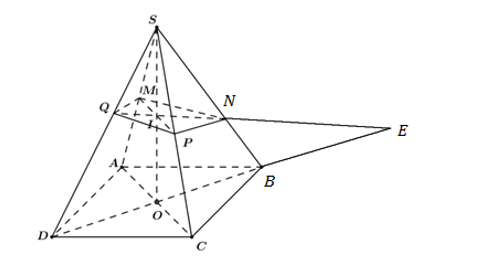
Gọi O là tâm hình bình hành ABCD
Gọi I là giao điểm của SO là và MP 
Trong mặt phẳng (SBD), kéo dài NI cắt SD tại Q, cắt BD tại E
Áp đụng định lý Menelaus trong tam giác SOB có: 
$\large \dfrac{MS}{MO}.\dfrac{EO}{EB}.\dfrac{NB}{NS}= 1\Leftrightarrow 1.\dfrac{EO}{EB}.\dfrac{1}{2}=1\Rightarrow  \dfrac{EO}{EB}=2\Rightarrow  \dfrac{ED}{EB}= 3$
Áp đụng định lý Menelaus trong tam giác SBD có:
 $\large \dfrac{QS}{QD}.\dfrac{ED}{EB}.\dfrac{NB}{NS}=1\Leftrightarrow \dfrac{QS}{QD}.3.\dfrac{1}{2}=1\Leftrightarrow \dfrac{QS}{QD}= \dfrac{2}{3}\Rightarrow  \dfrac{SQ}{SD}= \dfrac{2}{5}$