Cho hình chóp S.ABC có đyá ABC là tam giác vuông cân tại B; $\large BA
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có đyá ABC là tam giác vuông cân tại B; BA=a;SA=a√2 và SA vuông góc với mặt phẳng đáy. Góc giữa SC và mặt phẳng (SAB) bằng bao nhiêu?
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
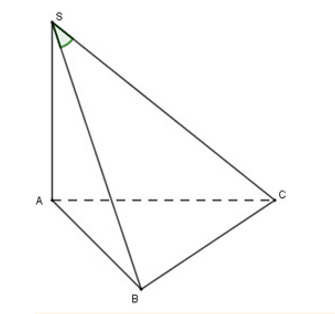
Ta có: {CB⊥ABCB⊥SA(doSA⊥(ABC)) ⇒CB⊥(SAB) tại B
Suy ra hình chiếu của SC lên mặt phẳng (SAB) là SB
Hay góc giữa SC và (SAB) là góc ^CSBVì\large \Delta ABCcântạiBnên\large BC= AB= aXéttamgiácSABvuôngtạiA\large \Rightarrow SB= \sqrt{SA^2+AB^2}= \sqrt{2a^2+a^2}= a\sqrt{3}XéttamgiácSBCvuôngtạiB(do\large BC\perp (SAB)\Rightarrow BC\perp SBcó\large \tan\widehat{CSB}= \dfrac{BC}{SB}= \dfrac{a}{a\sqrt{3}}= \dfrac{1}{\sqrt{3}}\Rightarrow \widehat{CSB} = 30^\circ $)
Xem thêm các bài tiếp theo bên dưới
- Cho hình lập phương ABCD.A’B’C’D’.Tính góc giữa hai đường thẳng AC và
- Cho tứ diện ABCD có BD=2, hai tam giác ABD, BCD có diện tích
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc
- Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh $\large AB= a,\, AD= 3
- Cho lăng trụ đứng ABC.A’B’C’ có $\large AB= AC= BB’= a,\, \widehat{BAC