Cho hình chóp S. ABC có đáy là tam giac vuông cận tại B, cạnh bên SA v

Cho hình chóp S. ABC có đáy là tam giac vuông cận tại B, cạnh bên SA vuông góc với mặt phẳng đáy, $\large AB= BC=a$ và $\large SA= a$. Góc giữa hai mặt phẳng (SAC) và (SBC) bằng 

• A. $\large 60^\circ $
• B. $\large 90^\circ $
• C. $\large 30^\circ $
• D. $\large 45^\circ $

Chọn A

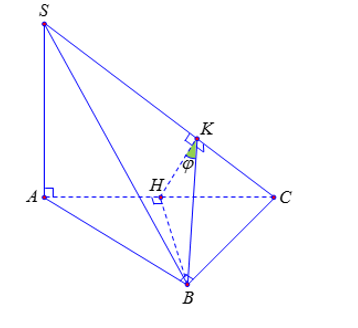
Gọi H là trung điểm cạnh AC
Ta có: $\large (SAC)\perp (ABC)$ (vì $\large SA\perp (ABC)$ và $\large BH\perp AC\Rightarrow  BH\perp (SAC)$)
Trong mặt phẳng (SAC), kẻ $\large HK\perp SC$ thì $\large SC\perp (BHK)\Rightarrow  SC\perp BK$
$\large \Rightarrow  \angle ((SAC), (SBC))= \angle SKH= \varphi$
Mặt khác: 
Tam giác ABC vuông cân tại B có $\large AB= BC= a$ nên $\large AC= a\sqrt{2}$ và $\large BH= \dfrac{a\sqrt{2}}{2}$
Hai tam giác CKH và CAS đồng dạng nên $\large HK= \dfrac{HC.SA}{SC}$
$\large \Leftrightarrow HK= \dfrac{HC.SA}{\sqrt{SA^2+AC^2}}= \dfrac{a\sqrt{2}}{\sqrt{3}}$
Tam giác BHK vuông tại H có $\large \tan \varphi = \dfrac{BH}{BK}=\sqrt{3}\Rightarrow  \varphi = 60^\circ $
Vậy $\large \angle ((SAC), (SBC))= 60^\circ $