Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng a, $\large S
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng a, SA⊥(ABCD),SA=a√3. Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng AB và CM
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
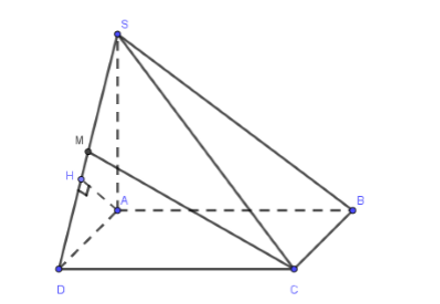
AB//CD⇒AB//(SCD)⊃CM
⇒d(AB,CM)=d(AB,(SCD))=d(A,(SCD))
Kẻ AH⊥SD,H∈SD (1), ta có:
{CD⊥ADCD⊥SA ⇒CD⊥(SAD)⇒SD⊥AD (2)
Từ (1) và (2) ⇒d(A,(SCD))=AH⇒d(AB,CM)=AH
Tam giác SAD vuông tại A, AH⊥SD,H∈SD, suy ra:
1AH2=1SA2+1AD2=1(a√3)2+1a2=43a2⇒AH2=3a24⇒AH=a√32
Vậy khoảng cách giữa 2 đường thẳng CM và AB là a√32
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S. ABC có đáy là tam giac vuông cận tại B, cạnh bên SA v
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a và $\large
- Cho hình chóp S.ABC có đyá ABC là tam giác vuông cân tại B; $\large BA
- Cho hình lập phương ABCD.A’B’C’D’.Tính góc giữa hai đường thẳng AC và
- Cho tứ diện ABCD có BD=2, hai tam giác ABD, BCD có diện tích