Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có $\large A

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có $\large AB=4cm$. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với (ABC). Lấy M thuộc SC sao cho $\large CM= 2MS$. Khoảng cách giữa hai đường thẳng AC và BM là: 

• A. $\large \dfrac{4\sqrt{21}}{7}\, cm$
• B. $\large \dfrac{8\sqrt{21}}{21}\, cm$
• C. $\large \dfrac{4\sqrt{21}}{21}\, cm$
• D. $\large \dfrac{2\sqrt{21}}{3}\, cm$

Chọn A

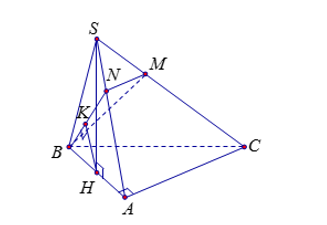
Cách 1: 
Gọi H là trung điểm của AB, suy ra $\large SH\perp (ABC)$
Trong (SAC) từ M dựng $\large MN//AC$, gọi K là hình chiếu của H trên BN
Ta có: $\large AC\perp (SAB)$ mà $\large MN//AC\Rightarrow  MN\perp (SAB)$
$\large \left\{\begin{align}& HK\perp BN\\& HK\perp MN\\\end{align} \right.$ $\large \Rightarrow  HK\perp (MNB)$
Vì $\large (BMN)//AC$ suy ra khoảng cách giữa hai đường AC và BM là $\large d(A, (MNN))= 2d(H, (BMN))= 2HK= 2BH.\sin\widehat{ABN}$
Trong tam giác SAB hạ $\large NF\perp AB$, suy ra: $\large NF= \dfrac{2}{3}SH= \dfrac{2}{3}.\dfrac{4\sqrt{3}}{2}=\dfrac{4\sqrt{3}}{3}$ và $\large BF=BH+HF=BH+\dfrac{1}{3}.AH=2+\dfrac{2}{3}= \dfrac{8}{3}$
Vậy $\large BN=\sqrt{BF^2+NF^2}= \dfrac{a\sqrt{7}}{3};\, \dfrac{BN}{\sin 60^\circ}= \dfrac{AN}{\sin\widehat{ABN}}$
$\large \Leftrightarrow \sin\widehat{ABN}= \dfrac{\dfrac{2a}{3}.\dfrac{\sqrt{3}}{2}}{\dfrac{a\sqrt{7}}{3}}=\dfrac{\sqrt{7}}{\sqrt{3}}$
Suy ra: $\large d(A, (BMN))= 2.2.\dfrac{\sqrt{3}}{\sqrt{7}}= \dfrac{4\sqrt{21}}{7}$