Cho hình lăng trụ tam giác ABC.A'B'C' có đáy là tam giác vuông tại A,
MỤC LỤC
Câu hỏi:
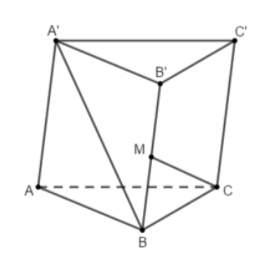
Cho hình lăng trụ tam giác ABC.A'B'C' có đáy là tam giác vuông tại A, AB=2,AC=√3AB=2,AC=√3. Góc ^CAA′=90∘,^BAA′=120∘. Gọi M là trung điểm cạnh BB' (hình vẽ). Biết CM vuông góc với A'B. Tính thể tích khối lăng trụ đã cho

Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
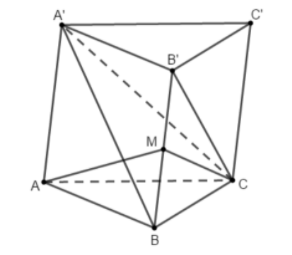
Do AC⊥AB,AC⊥AA′ nên AC⊥(ABB′A′). Mà A′B⊂(ABB′A′) nên AC⊥A′B
Có A′B⊥AC,A′B⊥CM nên A′B⊥(AMC)⇒A′B⊥AM
Đặt AA′=x,(x>0). Ta có: →A′B=→AB−→AA′ và →AM=→AB+→BM=→AB+12→AA′
Suy ra: →A′B.→AM=(→AB−→AA′)(→AB+12→AA′)=AB2−12AA′2−12→AB.→AA′
=AB2−12AA′2−12AB.AA′.cosBAA′=22−12x2−12.2.x.cos120∘=−12x2+12x+4
Do: A′B⊥AM nên →A′B.→AM=0⇔−12x2+12x+4=0⇒x=1+√332
Lại có SABB′A′=AB.AA′.sinBAA′=2.1+√332.sin120∘=√3(1+√33)2(dvdt)
Do AC⊥(ABB′A′) nên VC.ABB′A′=13.AC.SABB′A′=13.√3.√3(1+√33)2=1+√332(dvdt)
mà VC.A′B′C′=13VABC.A′B′C′⇒VC.ABB′A′=VABC.A′B′C′−VC.A′B′C′=23VABC.A′B′C′
Vậy: VABC.A′B′C′=32VC.ABB′A′=32.1+√332=3(1+√33)4(dvdt)
Xem thêm các bài tiếp theo bên dưới
- Tìm tất cả các giá trị thực của tham số m để phương trình $\large \log
- Có bao nhiêu giá trị nguyên của tham số m để hàm số $\large y=\dfrac{x
- Cho hàm số y=√1−lnx+1√1−lnx+m. Có b
- Gọi S là tập hợp các giá trị của tham số m sao cho hai phương trình $\
- Biết phương trình x4+ax3+bx2+cx+1=0 có nghiệm. Tìm giá trị