Có bao nhiêu giá trị nguyên của tham số m để hàm số $\large y=\dfrac{x

Có bao nhiêu giá trị nguyên của tham số m để hàm số $\large y=\dfrac{x^2+2x+m}{x-1}$ nghịch biến trên khoảng $\large (1; 3)$ và đồng biến trên khoảng $\large (4; 6)$

• A. A. 6
• B. B. 7
• C. C. 5
• D. D. 4

Chọn D

Ta có: $\large y'=\dfrac{x^2-2x-2-m}{(x-1)^2}$

Hàm số nghịch biến trên khoảng $\large (1; 3)$ và đồng biến trên khoảng $\large (4; 6)$ khi và chỉ khi 

$\large \left\{\begin{align}& y'\leq 0,\, \forall x\in (1; 3)\\& y'\geq 0,\, \forall x\in (4; 6)\\\end{align}\right.$

$\large \Leftrightarrow\left\{\begin{align}& x^2-2x-2-m\leq 0,\, \forall x\in (1; 3)\\& x^2-2x-2-m\geq 0,\, \forall x\in (4; 6)\\\end{align}\right.$ $\large \Leftrightarrow\left\{\begin{align}& m\geq x^2-2x-2, \forall x\in (1; 3)\\& x\leq x^2-2x-2, \forall x\in (4; 6)\\\end{align}\right.$ 

Xét hàm số $\large g(x)=x^2-2x-2, g'(x)=2x-2$ ta có bảng biến thiên của g(x) như sau: 

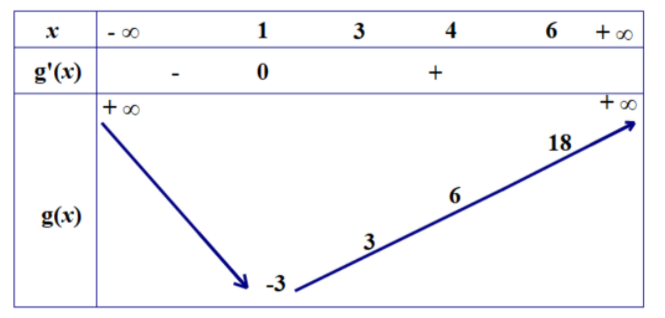
Từ bảng biến thiên của  g(x) ta có: $\large (*)\Leftrightarrow 3\leq m\leq 6$, và vì m là số nguyên nên $\large m\in\left\{3; 4; 5; 6\right\}$

Vậy có 4 giá trị nguyên của m thỏa mãn bài toán