Cho hàm số $\large y=\dfrac{\sqrt{1-\ln x}+1}{\sqrt{1-\ln x}+m}$. Có b

Cho hàm số $\large y=\dfrac{\sqrt{1-\ln x}+1}{\sqrt{1-\ln x}+m}$. Có bao nhiêu giá trị nguyên của tham số m thuộc $\large [-5; 5]$ để hàm số đã cho đồng biến trên khoảng $\large \left(\dfrac{1}{e^3}; 1\right)$

• A. A. 7
• B. B. 6
• C. C. 5
• D. D. 4

Chọn B

Ta có đạo hàm của $\large y=\dfrac{\sqrt{1-\ln x}+1}{\sqrt{1-\ln x}+m}$ là $\large y'=\dfrac{1-m}{2x\sqrt{1-\ln x}(\sqrt{1-\ln x}+m)^2}$

Hàm số đã cho đồng biến trên khoảng $\large \left(\dfrac{1}{e^3}; 1\right)$ khi và chỉ khi $\large y'>0,\forall x\in \left(\dfrac{1}{e^3}; 1\right)$

$\large \Leftrightarrow \left\{\begin{align}& 1-m>0\\& \sqrt{1-\ln x}+m\neq 0, \forall x\in \left(\dfrac{1}{e^3}; 1\right)\\\end{align}\right. $ $\large \Leftrightarrow \left\{\begin{align}& m<1\\& \sqrt{1-\ln x}+m\neq 0, \forall x\in \left(\dfrac{1}{e^3}; 1\right)\,\, (*)\\\end{align}\right. $ 

Xét hàm số $\large g(x)=\sqrt{1-\ln x}, x\in \left(\dfrac{1}{e^3}; 1\right)$, ta có: $\large g'(x)=\dfrac{-1}{2x\sqrt{1-\ln x}}, \forall x\in \left(\dfrac{1}{e^3}; 1\right)$ do đó ta có bảng biến thiên của hàm số g(x) như sau: 

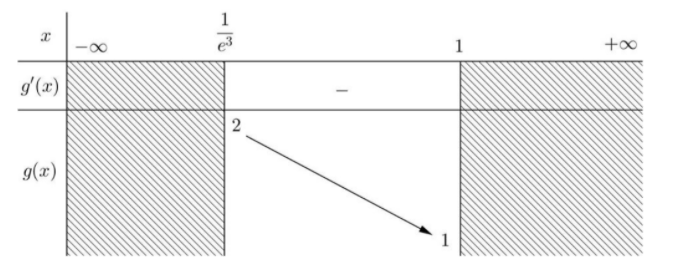
Qua bảng biến thiên ta có: $\large (*)\Leftrightarrow \left\{\begin{align}& m<1\\& x\notin (-2; -1)\\\end{align}\right. $, kết hợp với $\large [5; -5]$ ta có 6 giá trị nguyên của m là $\large m\in\left\{-5; -4; -3; -2; -1; 0\right\}$