Tìm tất cả các giá trị thực của tham số m để phương trình $\large \log

Tìm tất cả các giá trị thực của tham số m để phương trình $\large \log_3x+\sqrt{\log_3x+1}-2m-1=0$ có ít nhất một nghiệm thực trong đoạn $\large [1; 27]$

• A.

  A. $\large m\in (0; 2)$

• B.

  B. $\large m\in [0; 2]$

• C.

  C. $\large m\in [2; 4]$

• D.

  D. $\large m\in (0; 4)$

Chọn B

Đặt $\large t=\sqrt{\log_3x+1}$. Với $\large x\in [1; 27]$ thì $\large t\in [1; 2]$

Phương trình đã cho trở thành $\large t^2+t-2m-2=0\Leftrightarrow 2m+2=t^2+t$ (*)

Xét hàm số $\large f(t)=t^2+t$ trên đoạn $\large [1; 2]$

Ta có: $\large f'(t)=2t+1>0, \forall t\in [1; 2]$ nên hàm số $\large f(t)=t^2+t$ đồng biến trên $\large [1; 2]$

Bảng biến thiên

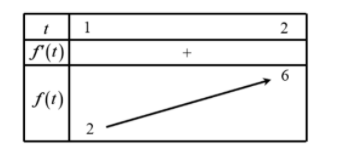
Để phương trình đã cho có it nhất một nghiệm thực trong đoạn $\large [1; 27]$ thì phương trình (*) phải có ít nhất một nghiệm thực trong đoạn $\large (1; 3)$

Từ bảng biến thiên, suy ra: $\large 2\leq 2m+2\leq 6\Leftrightarrow 0\leq m\leq 2$