Cho hình lăng trụ đứng $\Large ABC.{A}'{B}'{C}'$ có đáy là tam giác $\

Cho hình lăng trụ đứng $\Large ABC.{A}'{B}'{C}'$ có đáy là tam giác $\Large ABC$ vuông cân tại $\Large A$, cạnh $\Large BC=a\sqrt{6}$. Góc giữa mặt phẳng $\Large \left( A{B}'C \right)$ và mặt phẳng $\Large \left( BC{C}'{B}' \right)$ bằng $\Large 60{}^\circ $ . Tính thể tích $\Large V$ của khối đa diện $\Large A{B}'C{A}'{C}'$.

• A. $\Large {{a}^{3}}\sqrt{3}$.
• B. $\Large \dfrac{3{{a}^{3}}\sqrt{3}}{2}$.
• C. $\Large \dfrac{{{a}^{3}}\sqrt{3}}{2}$.
• D. $\Large \dfrac{{{a}^{3}}\sqrt{3}}{3}$.

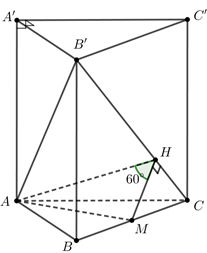
Khối đa diện $\Large A{B}'C{A}'{C}'$ là hình chóp $\Large {B}'.AC{C}'{A}'$ có

$\Large{A}'{B}' \perp \left( AC{C}'{A}' \right)$.

Từ giả thiết tam giác $\Large ABC$ vuông cân tại $\Large A$, cạnh $\Large BC=a\sqrt{6}$ ta suy ra $\Large AB=AC=a\sqrt{3}$.

Gọi $\Large M$ là trung điểm của $\Large BC$, suy ra $\Large AM\bot BC$ và $\Large AM=\dfrac{a\sqrt{6}}{2}$.

Ta có $\Large \left\{ \begin{matrix}& AM\bot BC \\ & AM\bot B{B}' \\ \end{matrix} \right.\Rightarrow AM\bot \left( BC{C}'{B}' \right)\Rightarrow AM\bot {B}'C$ (1).

Gọi $\Large H$ là hình chiếu vuông góc của $\Large M$ lên $\Large {B}'C$, suy ra $\Large MH\bot {B}'C$ (2).

Từ (1) và (2) ta suy ra $\Large {B}'C\bot \left( AMH \right)$. Từ đó suy ra góc giữa mặt phẳng $\Large \left( A{B}'C \right)$ và mặt phẳng $\Large \left( BC{C}'{B}' \right)$ là góc giữa $\Large AH$ và $\Large MH$. Mà tam giác $\Large AMH$ vuông tại $\Large H$ nên $\Large \Rightarrow \widehat{AHM}=60{}^\circ $.

$\Large \Rightarrow MH=AM.\cot 60{}^\circ =\dfrac{a\sqrt{6}}{2}.\dfrac{1}{\sqrt{3}}=\dfrac{a\sqrt{2}}{2}$.

Tam giác $\Large {B}'BC$ đồng dạng với tam giác $\Large MHC$ nên suy ra $\Large \sin \widehat{HCM}=\dfrac{MH}{MC}=\dfrac{\dfrac{a\sqrt{2}}{2}}{\dfrac{a\sqrt{6}}{2}}=\dfrac{1}{\sqrt{3}}$

$\Large \Rightarrow 1+{{\tan }^{2}}\widehat{MCH}=\dfrac{1}{1-{{\sin }^{2}}\widehat{MCH}}=\dfrac{1}{1-\dfrac{1}{3}}=\dfrac{3}{2}$$\Large \Rightarrow \tan \widehat{MCH}=\dfrac{\sqrt{2}}{2}$

$\Large \Rightarrow B{B}'=BC.\tan \widehat{MCH}=a\sqrt{6}.\dfrac{\sqrt{2}}{2}=a\sqrt{3}$

$\Large \Rightarrow {{V}_{A{B}'C{A}'{C}'}}={{V}_{{B}'.AC{C}'{A}'}}$$\Large =\dfrac{1}{3}{B}'{A}'.AC.A{A}'=\dfrac{1}{3}.a\sqrt{3}.a\sqrt{3}.a\sqrt{3}={{a}^{3}}\sqrt{3}$.