Cho đồ thị $\Large \left( C \right):y=f\left( x \right)=\sqrt{x}$. Gọi

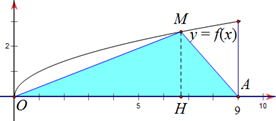
Cho đồ thị $\Large \left( C \right):y=f\left( x \right)=\sqrt{x}$. Gọi $\Large \left( H \right)$ là hình phẳng giới hạn bởi đồ thị $\Large \left( C \right)$, đường thẳng $\Large x=9$ và trục $\Large Ox$. Cho điểm $\Large M$ thuộc đồ thị $\Large \left( C \right)$ và điểm $\Large A\left( 9;\,0 \right)$. Gọi $\Large {{V}_{1}}$ là thể tích khối tròn xoay khi cho $\Large \left( H \right)$ quay quanh trục $\Large Ox$, $\Large {{V}_{2}}$ là thể tích khối tròn xoay khi cho tam giác $\Large AOM$ quay quanh trục $\Large Ox$. Biết rằng $\Large {{V}_{1}}=2{{V}_{2}}$. Tính diện tích $\Large S$ phần hình phẳng giới hạn bởi đồ thị $\Large \left( C \right)$ và đường thẳng $\Large OM$.

• A. $\Large S=3$.
• B. $\Large S=\dfrac{27\sqrt{3}}{16}$.
• C. $\Large S=\dfrac{3\sqrt{3}}{2}$.
• D. $\Large S=\dfrac{4}{3}$.

Ta có $\Large {{V}_{1}}=\text{ }\!\!\pi\!\!\text{ }\int\limits_{0}^{9}{{{\left( \sqrt{x} \right)}^{2}}\text{d}x} = \dfrac{81\pi }{2}$.

Gọi $\Large H$ là hình chiếu của $\Large M$ lên trục $\Large Ox$, đặt $\Large OH=m$ (với $\Large 0

Suy ra $\Large {{V}_{2}}=\dfrac{1}{3}\text{ }\!\!\pi\!\!\text{ }.M{{H}^{2}}.OH+\dfrac{1}{3}\text{ }\!\!\pi\!\!\text{ }.M{{H}^{2}}.AH$$\Large =\dfrac{1}{3}\text{ }\!\!\pi\!\!\text{ }.M{{H}^{2}}.OA$$=$$\Large 3m\text{ }\!\!\pi\!\!\text{ }$.

Theo giả thiết, ta có $\Large {{V}_{1}}=2{{V}_{2}}$ nên $\Large \dfrac{81\text{ }\!\!\pi\!\!\text{ }}{2}=6m\text{ }\!\!\pi\!\!\text{ }$$\Large \Leftrightarrow $ $\Large m=\dfrac{27}{4}$. Do đó $\Large M\left( \dfrac{27}{4};\,\dfrac{3\sqrt{3}}{2} \right)$.

Từ đó ta có phương trình đường thẳng $\Large OM$ là $\Large y=\dfrac{2\sqrt{3}}{9}x$.

Diện tích $\Large S$ phần hình phẳng giới hạn bởi đồ thị $\Large \left( C \right)$ và đường thẳng $\Large OM$ là

$\Large S=\int\limits_{0}^{\dfrac{27}{4}}{\left( \sqrt{x}-\dfrac{2\sqrt{3}}{9}x \right)\text{d}x}$$\Large =\left. \left( \dfrac{2}{3}x\sqrt{x}-\dfrac{\sqrt{3}}{9}{{x}^{2}} \right) \right|_{0}^{\dfrac{27}{4}}$$\Large =\dfrac{27\sqrt{3}}{16}$.