Cho hàm số $\Large y=f\left( x \right)$ liên tục trên đoạn $\Large \le

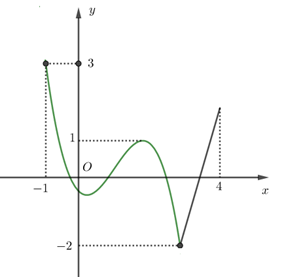
Cho hàm số $\Large y=f\left( x \right)$ liên tục trên đoạn $\Large \left[ -1;4 \right]$ và có đồ thị như hình vẽ.

Có bao nhiêu giá trị nguyên của $\Large m$thuộc đoạn $\Large \left[ -10;10 \right]$ để bất phương trình $\Large \left| f\left( x \right)+m \right|<2m$ đúng với mọi $\Large x$ thuộc đoạn $\Large \left[ -1;4 \right]$.

• A. $\Large 6$.
• B. $\Large 5$.
• C. $\Large 7$.
• D. $\Large 8$.

Chọn C

Để bất phương trình $\Large \left| f\left( x \right)+m \right|<2m$ có nghiệm ta suy ra điều kiện $\Large m>0$.

$\left| f\left( x \right)+m \right|<2m\Leftrightarrow -2m-3m \\ & f\left( x \right)

Bất phương trình $\Large \left| f\left( x \right)+m \right|<2m$ đúng với mọi $\Large x$ thuộc đoạn $\Large \left[ -1;4 \right]$ $\Large \Leftrightarrow \left\{ \begin{matrix}& f\left( x \right)>-3m \\ & f\left( x \right)

Với mọi $\Large x$ thuộc đoạn $\Large \left[ -1;4 \right]$ $\Large \Leftrightarrow \left\{ \begin{matrix}& -3m<\underset{\left[ -1;4 \right]}{\mathop{\min }}\,f\left( x \right) \\ & m>\underset{\left[ -1;4 \right]}{\mathop{\max }}\,f\left( x \right) \\ \end{matrix} \right.$.

Từ đồ thị hàm số $\Large y=f\left( x \right)$ ta suy ra  $\Large \underset{\left[ -1;4 \right]}{\mathop{\min }}\,f\left( x \right)=-2;\text{ }\underset{\left[ -1;4 \right]}{\mathop{\max }}\,f\left( x \right)=3$.

$\Large \Rightarrow \left\{ \begin{matrix}& -3m<\underset{\left[ -1;4 \right]}{\mathop{\min }}\,f\left( x \right) \\ & m>\underset{\left[ -1;4 \right]}{\mathop{\max }}\,f\left( x \right) \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}& -3m<-2 \\ & m>3 \\ \end{matrix} \right.$$\Large \Leftrightarrow \left\{ \begin{matrix}& m>\dfrac{2}{3} \\ & m>3 \\ \end{matrix} \right.\Leftrightarrow m>3$(thỏa mãn điều kiện $\Large m>0$ )

Vậy trên đoạn $\Large \left[ -10;10 \right]$ có $\Large 7$ giá trị nguyên của $\Large m$ thỏa mãn điều kiện bài toán.