Cho hai mặt phẳng (P),(Q) song

MỤC LỤC
Câu hỏi:
Cho hai mặt phẳng (P),(Q) song song với nhau và cùng cắt khối cầu tâm O, bán kính R thành hai hình tròn cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Tính khoảng cách h giữa hai mặt phẳng (P),(Q)để diện tích xung quanh của hình nón là lớn nhất.
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
Cắt khối cầu tâm O, bán kính Rbằng mặt phẳng (α) đi qua tâm O và vuông góc với hai mặt phẳng (P),(Q) ta được hình như hình vẽ bên dưới.
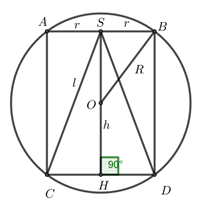
Trong đó, AB=(α)∩(P),CD=(α)∩(Q)với AB=CD, h=SH=AC=BD, R=OB.
Đường sinh l=SC=SD.
Bán kính của mỗi hình tròn giao tuyến làr=AB2.
Ta có: l2=SC2=AC2+AS2=h2+r2 vàr2=SB2=OB2−SO2=R2−h24.
Suy ra l2=R2+3h24.
Mà diện tích xung quanh của khối nón được xét là:Sxq=πrl.
Ta cóSxq đạt giá trị lớn nhất⇔rl đạt giá trị lớn nhất.
Áp dụng bất đẳng thức Cauchy cho 2 sốr√3 vàl ta có
rl=12√3.2.(r√3)l≤√36(3r2+l2)=√36.4R2=2R2√33.
rl lớn nhất là2R2√33 khi và chỉ khi3r2=l2⇔h2=43R2⇒h=2R√33.