Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi có cạnh 4a, $

Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi có cạnh  4a, $\Large A'A = 8a, \widehat{BAD} = 120°$. Gọi M , N , K lần lượt là trung điểm cạnh AB', B'C, BD'. Thể tích khối da diện lồi có các đỉnh là các điểm A, B, C, M, N, K  là:

• A.

  $\large 12 \sqrt {3} a^{3}$

• B.

  $\large \dfrac {28 \sqrt {3}}{3} a^{3}$ 

• C.

  $\large 16 \sqrt {3} a^{3}$

• D.

  $\large \dfrac {40 \sqrt {3}}{3} a^{3}$ 

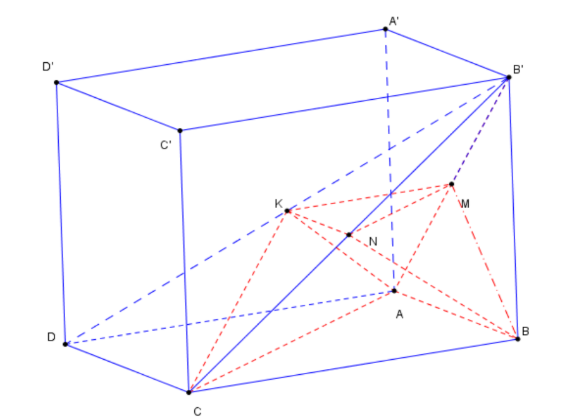$\large MN / / AC; MN = \dfrac {1}{2} AC$, MNCA là hình thang.
$\large V_{MNK.ABC} = V_{K.MNCA} + V_{B.MNCA}$
DK cắt (B'AC) tại B', $\large \dfrac {B'K}{B'D} =  \dfrac {1}{2} \Rightarrow  \dfrac {d(K; MNCA)}{d(D; MNCA)} =  \dfrac {1}{2} \Rightarrow   V_{K.MNCA} = \dfrac {1}{2} V_{D.MNCA}$
Mà: $\large V_{D.MNCA} = V_{B.MNCA}$ nên ta có: $\large V_{MNK.ABC} = \dfrac {1}{2} V_{B.MNCA} + V_{B.MNCA} = \dfrac {3}{2} V_{B.MNCA}$
Mặt khác $\large S_{MNCA} = \dfrac {3}{4} S_{B'AC} \Rightarrow V_{B.MNCA} = \dfrac {3}{4} V_{B.B'CA} = \dfrac {3}{4} . \dfrac {1}{6} V_{ABCD.A'B'C'D'} = 8 \sqrt {3} a^{3}$
$\large V_{MNK.ABC} = \dfrac {3}{2} V_{B.MNCA} =  \dfrac {3}{2} . 8 \sqrt {3} a^{3} = 12 \sqrt {3} a^{3}$