Cho hình lăng trụ ABC. A'B'C' có các cạnh đều bằng a. Tính diện tích S

Cho hình lăng trụ ABC. A'B'C' có các cạnh đều bằng a. Tính diện tích S của mặt cầu qua 6 đỉnh của hình lăng trụ đó

• A. A. $\large S=\dfrac{49\pi a^2}{144}$
• B. B. $\large S=\dfrac{7a^2}{3}$
• C. C. $\large S=\dfrac{7\pi a^2}{3}$
• D. D. $\large S=\dfrac{49a^2}{144}$

Chọn C

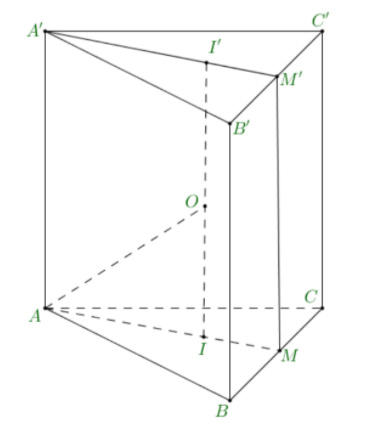
Gọi I, I' lần lượt là trọng tâm tam giác ABC và A'B'C, O là trung điểm II'

Khi đó O là tâm mặt cầu ngoại tiếp hình lăng trụ

Ta có: $\large AI=\dfrac{a\sqrt{3}}{3},\,\, OI=\dfrac{a}{2}$

Suy ra: $\large OA=\sqrt{\left(\dfrac{a\sqrt{3}}{3}\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{\sqrt{7}a}{\sqrt{12}}$

Diện tích mặt cầu ngoại tiếp hình lăng trụ là: $\large S=4\pi OA^2=\dfrac{7\pi a^2}{3}$