Cho hàm số $\large y=f(x)$ có đạo hàm đến cấp hai trên $\large \mathbb

Cho hàm số $\large y=f(x)$ có đạo hàm đến cấp hai trên $\large \mathbb{R}$ và có bảng xét dấu của hàm số $\large y=f'(x)$ như hình sau:

Hỏi hàm số $\large g(x)=f(1-x)+\dfrac{x^3}{3}-2x^2+3x$ đạt cực tiểu tại điểm nào trong các điểm sau?

• A.

  A. $\large x=3$

• B.

  B. $\large x=0$

• C.

  C. $\large x=-3$

• D.

  D. $\large x=1$

Chọn A
$\large g'(x)=-f(1-x)+x^2-4x+3$

$\large -f'(1-x)>0\Leftrightarrow f'(1-x)<0$ $\large \Leftrightarrow \left[\begin{align}& 1-x<-2\\& 0<1-x<4\\\end{align}\right. $ $\large \Leftrightarrow \left[\begin{align}& x>3\\& -3

Bảng xét dấu $\large g'(x)$

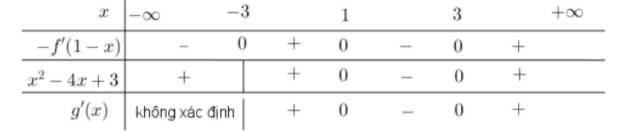
Từ bảng xét dấu $\large g'(x)$ ta suy ra hàm số đạt cực tiểu tại $\large x=3$