Cho hình chóp S.ABC có đáy ABC là tam giác cân, $\large BA=BC=a$ và $\

Cho hình chóp S.ABC có đáy ABC là tam giác cân, $\large BA=BC=a$ và $\large \widehat{BAC}=30^\circ$. Cạnh bên SA vuông góc với mặt phẳng đáy và $\large SA=a$. Gọi D là điểm đối xứng với B qua AC. Khoảng cách từ B đến mặt phẳng (SCD) bằng

• A.

  A. $\large \dfrac{2a\sqrt{21}}{7}$

• B.

  B. $\large \dfrac{a\sqrt{2}}{2}$

• C.

  C. $\large \dfrac{a\sqrt{21}}{14}$

• D.

  D. $\large \dfrac{a\sqrt{21}}{7}$

Chọn D

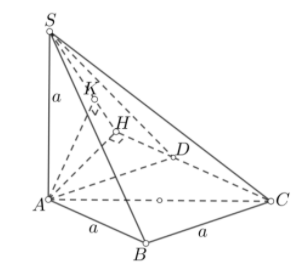
Tam giác ABC cận tại B có $\large BAC=30^\circ$ và D đối xứng với B qua AC nên tứ giác ABCD là hình thoi có $\large ADC=ABC=120^\circ$

Trong mặt phẳng (ABC), kẻ AH vuông góc với đường thẳng CD tại H. Khi đó $\large CD\perp AH$ và $\large CD\perp SA$ nên $\large CD\perp (SAH)$. Do đó: $\large (SCD)\perp (SAH)$

Trong mặt phẳng (SAH), kẻ $\large AK\perp SH$ tại K. Khi đó: $\large AK\perp (SCD)$ và $\large AK=d[A, (SCD)]$

Ta có: $\large AH=AD.\sin 60^\circ =\dfrac{a\sqrt{3}}{2}$

Áp dụng hệ thức lượng trong tam giác vuông SAH, ta có: $\large \dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{7}{3a^2}$

Từ đó: $\large AK=\dfrac{a\sqrt{21}}{7}$

Vì $\large AB// (SCD)$ nên $\large d[B, (SCD)]=d[A, (SCD)]=AK=\dfrac{a\sqrt{21}}{7}$