Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 1. Mặt bên (SAC) l

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 1. Mặt bên (SAC) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy, $\large SA=SC=\dfrac{3}{2}$. Gọi D là điểm đối xứng với B qua C. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABD

• A. A. $\large \dfrac{\sqrt{34}}{8}$
• B. B. $\large \dfrac{3\sqrt{34}}{4}$
• C. C. $\large \dfrac{3\sqrt{34}}{16}$
• D. D. $\large \dfrac{3\sqrt{34}}{8}$

Chọn C

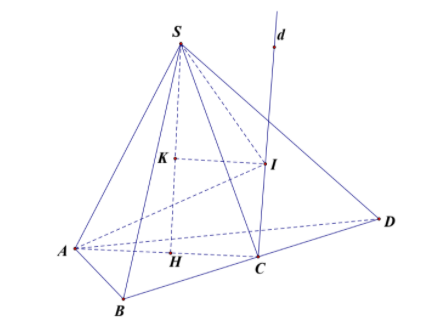
Gọi H là trung điểm của AC, do SAC là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy nên $\large SH\perp AC\Rightarrow SH\perp (ABC)$ và $\large SH=\sqrt{SA^2-AH^2}=\sqrt{\dfrac{9}{4}-\dfrac{1}{4}}=\sqrt{2}$

Tam giác ABD có AC là đường trung tuyến và $\large AC=\dfrac{1}{2}BD$ nên ABD là tam giác vuông tại A, suy ra C là tâm đường tròn ngoại tiếp tam giác ABD

Dựng trục (d) của đường tròn ngoại tiếp tam giác ABD. Gọi I là tâm của mặt cầu ngoại tiếp khối chóp S.ABD $\large \Rightarrow I\in d$ và $\large IA=IS=ID=IB=R$

Kẻ $\large IK\perp SH\Rightarrow IK=AH=\dfrac{1}{2}$

Giả sử $\large HK=x\Rightarrow SK=\sqrt{2}-x\Rightarrow IS=\sqrt{SK^2+HC^2}=\sqrt{(\sqrt{2}-x)^2+\dfrac{1}{4}}=R$

Mặt khác: $\large R=IA=\sqrt{AC^2+IC^2}=\sqrt{1+x^2}$

Ta có phương trình: $\large \sqrt{(\sqrt{2}-x)^2+\dfrac{1}{4}}=\sqrt{1+x^2}\Leftrightarrow x=\dfrac{5\sqrt{2}}{16}$

Suy ra: $\large R=\dfrac{3\sqrt{34}}{16}$