Cho hàm số $\large f(x)=x^4+ax^2+b$ có giá trị cực đại $\large y_{CD}=

Cho hàm số $\large f(x)=x^4+ax^2+b$ có giá trị cực đại $\large y_{CD}=9$ và giá trị cực tiểu $\large y_{CT}=1$. Hỏi có bao nhiêu giá trị nguyên của tham số m để phương trình $\large f(x^2)=m^2$ có 4 nghiệm phân biệt

• A. A. 2
• B. B. 7
• C. C. 1
• D. D. 6

Chọn C

Hàm số $\large f(xx^4+ax^2+b$ là hàm số trùng phương nên có giá trị cực đại $\large y_{CD}=9$ và giá trị cực tiểu $\large y_{CT}=1$, suy ra bảng biến thiên của  f(x) như sau: 

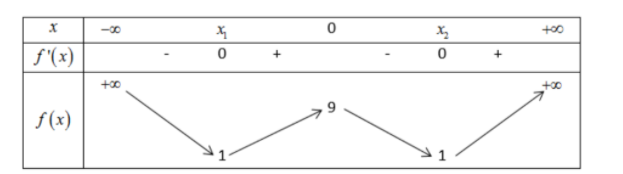
Đặt $\large t=x^2,\, (t\geq 0)$ phương trình $\large f(x^2)=m$ trở thành $\large f(t)=m$. Phương trình $\large f(x^2)=m$ có 4 nghiệm phân biệt khi và chỉ khi phương trình $\large f(t)=m^2$ có 2 nghiệm $\large t>0$

Dựa vào bảng biến thiên của hàm số f(x) trên nửa khoảng $\large [0; +\infty)$, phương trình $\large f(t)=m^2$ có 2 nghiệm $\large t>0$ khi và chỉ khi $\large 1

Vậy có 1 số nguyên m thỏa mãn yêu cầu bài toán