Cho hình hộp đứng $\Large ABCD.A'B'C'D'$ có $\Large AB=5a$, $\Large AD

Cho hình hộp đứng $\Large ABCD.A'B'C'D'$ có $\Large AB=5a$, $\Large AD=6a$, $\Large BD=7a$, $\Large AA'=\dfrac{12\sqrt{6}a}{7}$. Khoảng cách giữa hai đường thẳng $\Large A'B$ và $\Large B'C$ là

• A.

  $\Large \dfrac{12a}{7}$.

• B.

  $\Large \dfrac{12a\sqrt{2}}{7}$.

• C.

  $\Large \dfrac{12a\sqrt{6}}{7}$.

• D.

  $\Large \dfrac{12a\sqrt{3}}{7}$.

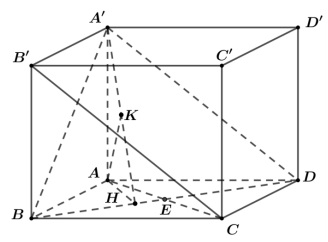
+ Trong $\Large (ABCD)$ gọi $\Large AC\cap BD=E$.

+ Vì $\Large \left\{\begin{align} & CD// AB// A'B' \\ & CD=AB=A'B'=5a \end{align}\right.$ $\Large \Rightarrow CDA'B'$ là hình bình hành.

+ Ta có $\Large B'C// A'D\Rightarrow B'C// (A'BD)$ $\Large \Rightarrow d(B'C, BA')=d\big(B'C, (A'BD)\big)$

=$\Large d\big(C, (A'BD)\big)=d\big(A, (A'BD)\big)$ (vì $\Large E$ là trung điểm $\Large AC$).

+ Trong $\Large (ABCD)$ kẻ $\Large AH\perp BD$ tại $\Large H$, lại có $\Large AA'\perp BD$, suy ra $\Large BD\perp (A'AH)\Rightarrow (A'AH)\perp (A'BD)$ (1).

+ Mặt khác $\Large (A'AH)\cap (A'BD)=A'H$ (2).

+ Trong $\Large (A'AH)$ kẻ $\Large AK\perp A'H$ tại $\Large K$ (3).

+ Từ (1), (2), (3) $\Large \Rightarrow AK\perp (A'BD)\Rightarrow d\big(A, (A'BD)\big)=AK$.

+ $\Large p=\dfrac{AB+AD+BD}{2}=9a$ $\Large \Rightarrow S_{\Delta ABD}=\sqrt{p(p-AB)(p-AD)(p-BD)}=6\sqrt{6}a^2$.

+ Mặt khác $\Large S_{\Delta ABD}=\dfrac{1}{2}.AH.BD$ $\Large \Leftrightarrow AH=\dfrac{2S_{\Delta ABD}}{BD}=\dfrac{12a\sqrt{6}}{7}$.

+ Vì $\Large AA'=AH=\dfrac{12a\sqrt{6}}{7}$, suy ra $\Large \Delta A'AH$ vuông cân tại $\Large A$ ($\Large K$ trung điểm $\Large A'H$)

$\Large \Rightarrow AK=\dfrac{1}{2}A'H=\dfrac{1}{2}.\dfrac{12a\sqrt{6}}{7}.\sqrt{2}=\dfrac{12a\sqrt{3}}{7}$.

Vậy khoảng cách giữa hai đường thẳng $\Large A'B$ và $\Large B'C$ là $\Large \dfrac{12a\sqrt{3}}{7}$.