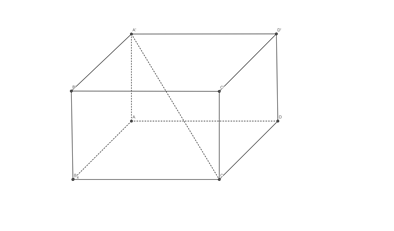
Cho hình hộp chữ nhật $\Large ABC\text{D}.A'B'C'D'$ có $\Large AB=a$,

Cho hình hộp chữ nhật $\Large ABC\text{D}.A'B'C'D'$ có $\Large AB=a$, $\Large A\text{D}=2\sqrt{2}a$,  $\Large AA'=\sqrt{3}a$ (tham khảo hình bên). Góc giữa đường thẳng $\Large A'C$ và mặt phẳng $\Large \left( ABC\text{D} \right)$ bằng

• A. $\Large {{45}^{{}^\circ }}$.
• B. $\Large {{90}^{{}^\circ }}$.
• C. $\Large {{60}^{{}^\circ }}$.
• D. $\Large {{30}^{{}^\circ }}$.

Chọn D

Ta thấy: hình chiếu của $\Large A'C$ xuống $\Large \left( ABC\text{D} \right)$ là $\Large AC$ do đó $\Large \left( A'C;\left( ABC\text{D} \right) \right)=\left( A'C;AC \right)=\widehat{A'CA}$.

Ta có: $\Large AC=\sqrt{A{{B}^{2}}+A{{\text{D}}^{2}}}=3\text{a}$.

Xét tam giác $\Large A'CA$ vuông tại $\Large C$ ta có:

$\Large \tan \left( A'CA \right)=\dfrac{A'A}{AC}=\dfrac{\sqrt{3}a}{3a}=\dfrac{\sqrt{3}}{3}$

$\Large \Rightarrow \widehat{A'CA}={{30}^{{}^\circ }}$.