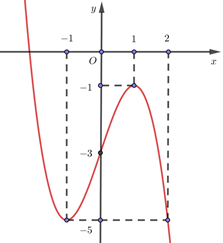
Cho hàm số $\Large y=f\left( x \right)$ có đồ thị như hình vẽ. Tích gi

Cho hàm số $\Large y=f\left( x \right)$ có đồ thị như hình vẽ.

Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số $\Large y=f\left( x+\sqrt{{{x}^{2}}-x+1}-1 \right)$ trên đoạn $\Large \left[ 0;1 \right]$ bằng:

• A. $\Large 3$.
• B. $\Large 15$.
• C. $\Large 5$.
• D. $\Large 0$.

Chọn A
Ta có: $\Large {f}'\left( x \right)=0\Leftrightarrow \left[ \begin{matrix}
& x=-1 \\ 
& x=1 \\ 
\end{matrix} \right.$.
$\Large {y}'=\left( 1+\dfrac{2x-1}{2\sqrt{{{x}^{2}}-x+1}} \right).{f}'\left( x+\sqrt{{{x}^{2}}-x+1}-1 \right)$.
$\Large {y}'=0\Leftrightarrow \left[ \begin{matrix}
& 2\sqrt{{{x}^{2}}-x+1}=1-2x\left( 1 \right) \\ 
& x+\sqrt{{{x}^{2}}-x+1}-1=-1\left( 2 \right) \\ 
& x+\sqrt{{{x}^{2}}-x+1}-1=1\left( 3 \right) \\ 
\end{matrix} \right.$.
$\Large \left( 1 \right)\Leftrightarrow \left\{ \begin{matrix}
& 1-2x\ge 0 \\ 
& 4\left( {{x}^{2}}-x+1 \right)={{\left( 1-2x \right)}^{2}} \\ 
\end{matrix} \right.$$\Large \Leftrightarrow \left\{ \begin{matrix}
& x\le \dfrac{1}{2} \\ 
& 4=1 \\ 
\end{matrix} \right.\left( VN \right)$.
$\Large \left( 2 \right)\Leftrightarrow \sqrt{{{x}^{2}}-x+1}=-x$$\Large \Leftrightarrow \left\{ \begin{matrix}
& x\le 0 \\ 
& {{x}^{2}}-x+1={{x}^{2}} \\ 
\end{matrix} \right.$$\Large \Leftrightarrow \left\{ \begin{matrix}
& x\le 0 \\ 
& x=1 \\ 
\end{matrix} \right.\left( VN \right)$.
$\Large \left( 3 \right)\Leftrightarrow \sqrt{{{x}^{2}}-x+1}=2-x$$\Large \Leftrightarrow \left\{ \begin{matrix}
& 2-x\ge 0 \\ 
& {{x}^{2}}-x+1=4-4x+{{x}^{2}} \\ 
\end{matrix} \right.$$\Large \Leftrightarrow x=1$.
$\Large \Rightarrow {y}'=0\Leftrightarrow x=1\notin \left( 0;1 \right)$.
$\Large y\left( 0 \right)=f\left( 0 \right)=-3$; $\Large y\left( 1 \right)=f\left( 1 \right)=-1$
$\Large \Rightarrow m=\underset{\left[ 0;1 \right]}{\mathop{\min }}\,f\left( x+\sqrt{{{x}^{2}}-x+1}-1 \right)=-3$ và $\Large \underset{\left[ 0;1 \right]}{\mathop{M=\max }}\,f\left( x+\sqrt{{{x}^{2}}-x+1}-1 \right)=-1$.
Vậy $\Large m.M=3$.