Cho hình hộp chữ nhật $\large ABCD.A'B'C'D'$. Khoảng cách giữa $\large

Cho hình hộp chữ nhật $\large ABCD.A'B'C'D'$. Khoảng cách giữa $\large AB$ và $\large B'C$ là $\large\dfrac{2a\sqrt{5}}{5}$, giữa $\large BC$ và $\large AB'$ là $\large\dfrac{2a\sqrt{5}}{5}$, giữa $\large AC$ và $\large BD'$ là $\large\dfrac{a\sqrt{3}}{3}$. Thể tích của khối hộp đó là:

• A.

  A. $\large 2a^{3}$

• B.

  B. $\large a^{3}$

• C.

  C. $\large 8a^{3}$

• D.

  D. $\large 4a^{3}$

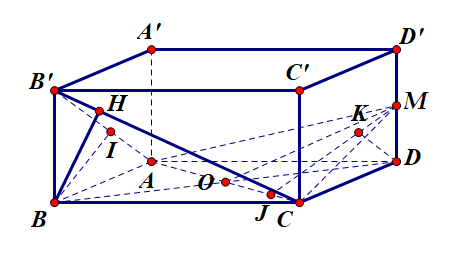
Đặt $\large AB=x,AD=y,AA'=z$

Gọi $\large H$ là hình chiếu vuông góc của $\large B$ trên $\large B'C$, ta có $\large BH$ là đoạn vuông góc chung của $\large AB$ và $\large B'C$ nên $\large d(AB,B'C)=BH=\dfrac{2a\sqrt{5}}{5}\Rightarrow \dfrac{1}{BH^{2}}=\dfrac{1}{z^{2}}+\dfrac{1}{y^{2}}=\dfrac{5}{4a^{2}}$ (1)

Gọi $\large I$ là hình chiếu vuông góc của $\large B$ trên $\large AB'$, ta có $\large BI$ là đoạn vuông góc chung của $\large BC$ và $\large AB'$ nên $\large d(BC,AB')=BI\Rightarrow \dfrac{1}{BI^{2}}=\dfrac{1}{x^{2}}+\dfrac{1}{z^{2}}=\dfrac{5}{4a^{2}}$ (2)

Gọi $\large M$ là trung điểm của $\large DD', O$ là giao điểm của $\large AC$ và $\large BD$, ta có mặt phẳng $\large (ACM)$ chứa $\large AC$ và song song với $\large BD'$ nên $\large d(AC,BD')=d(BD',(ACM))=d(D',(ACM))$.

Gọi $\large J$ là hình chiếu vuông góc của $\large D$ trên $\large AC, K$ là hình chiếu vuông của $\large D$ trên $\large MJ$, ta có $\large d(D',(ACM))=d(D,(ACM))=DK\Rightarrow \dfrac{1}{DK^{2}}=\dfrac{1}{x^{2}}+\dfrac{1}{y^{2}}+\dfrac{4}{z^{2}}=\dfrac{3}{a^{2}}$ (3)

Từ (1), (2) và (3) ta có $\large\dfrac{2}{z^{2}}=\dfrac{1}{2a^{2}}\Leftrightarrow z=2a\Rightarrow x=y=a$

Thể tích khối hộp là $\large V=xyz=2a^{3}$

Đáp án A