Cho tứ diện $\large ABCD$ có $\large BD=3$. Hai tam giác $\large ABD$

Cho tứ diện $\large ABCD$ có $\large BD=3$. Hai tam giác $\large ABD$ và $\large CBD$ có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện $\large ABCD$ bằng 11, số đo góc giữa hai mặt phẳng $\large (ABD)$ và $\large (CBD)$ là:

• A.

  A. $\large\arcsin \left ( \dfrac{11}{40} \right )$

• B.

  B. $\large\arcsin \left ( \dfrac{33}{40} \right )$

• C.

  C. $\large\arccos \left ( \dfrac{11}{40} \right )$

• D.

  D. $\large\arccos \left ( \dfrac{33}{40} \right )$

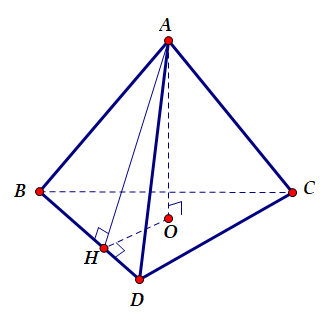
Kẻ $\large AH\perp BD$. Gọi $\large O$ là chân đường cao của tứ diện hạ từ đỉnh $\large A$

Suy ra $\large ((ABD);(CBD))=(AH;OH)=\widehat{AHO}$

Ta có $\large S_{\bigtriangleup ABD}=\dfrac{1}{2}BD.AH=6 \rightarrow AH=4$

${{V}_{ABCD}}=\dfrac{1}{3}{{S}_{\vartriangle BCD}}.AO\Rightarrow AO=\dfrac{3{{V}_{ABCD}}}{{{S}_{\vartriangle BCD}}}=\dfrac{33}{10}$

Xét tam giác vuông $\large AOH$, ta có 

$\large\sin \widehat{AHO}=\dfrac{AO}{AH}=\dfrac{33}{40}\rightarrow \widehat{AHO}=\arcsin \left ( \dfrac{33}{40} \right )$

Đáp án B