Cho hình chóp $\large S. ABC$có đáy $\large ABC$ là tam giác vuông cân

Cho hình chóp $\large S. ABC$có đáy $\large ABC$ là tam giác vuông cân tại $\large B,AB=BC=2a$, hai mặt phẳng $\large (SAB)$ và $\large (SAC)$ cùng vuông góc với mặt phẳng $\large (ABC)$. Gọi $\large M$ là trung điểm của $\large AB$, mặt phẳng qua $\large SM$ và song song với $\large BC$, cắt $\large AC$ tại $\large N$. Biết góc giữa hai mặt phẳng $\large (SBC)$ và $\large (ABC)$ bằng $\large 60^{\circ}$. Tính khoảng cách giữa hai đường thẳng $\large AB$ và $\large SN$ theo $\large a$

 

• A.

  A. $\large\dfrac{2a\sqrt{39}}{13}$

• B.

  B. $\large\dfrac{a\sqrt{39}}{13}$

• C.

  C. $\large\dfrac{a\sqrt{13}}{13}$

• D.

  D. $\large\dfrac{a\sqrt{13}}{26}$

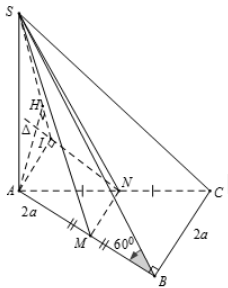
Ta có $\large\left\{\begin{align}(SAB)\perp (ABC)\\ (SAC)\perp (ABC)\end{align}\right.$ $\large\Rightarrow SA\perp (ABC)\Rightarrow CB\perp (SAB)$

Khi đó: $\large\left ( \widehat{(SBC),(ABC)} \right )=\widehat{SBA}=60^{\circ}$

$\large\Rightarrow SA=AB\cdot \tan 60^{\circ}=2a\sqrt{3}$

Ta có $\large AB//IN\Rightarrow AB//(SIN)\Rightarrow d(AB,SN)=d(AB,(SIN))=d(A,(SIN))$ (1)

Từ $\large N$ kẻ đường thẳng $\large\bigtriangleup $, song song với $\large AB$

Kẻ $\large AI\perp \bigtriangleup (I\in \bigtriangleup )$, kẻ $\large AH\perp SI(H\in SI)\Rightarrow d(A,(SIN))=AH$ (2)

Ta có $\large AINM$ là hình chữ nhật, nên $\large AI=MN=\dfrac{BC}{2}=a$

Xét tam giác $\large SAI$ ta có:

$\large\dfrac{1}{AH^{2}}=\dfrac{1}{AI^{2}}+\dfrac{1}{AS^{2}}=\dfrac{1}{a^{2}}+\dfrac{1}{12a^{2}}=\dfrac{13}{12a^{2}}\Rightarrow AH=\dfrac{2a\sqrt{39}}{13}$ (3)

Từ (1), (2) và (3) suy ra $\large d(AB,SN)=\dfrac{2a\sqrt{39}}{13}$

Đáp án A