Cho hình chóp đều $\large S.ABCD$ đáy tâm $\large O$ và có cạnh bằng $

Cho hình chóp đều $\large S.ABCD$ đáy tâm $\large O$ và có cạnh bằng $\large a$. Gọi $\large M,N$ lần lượt là trung điểm của $\large SA, BC$. Biết góc giữa $\large MN$ và $\large (ABCD)$ bằng $\large 60^{\circ}$. Tính sin của góc tạo bởi $\large MN$ và mặt phẳng $\large (SAC)$

• A.

  A. $\large\dfrac{\sqrt{5}}{5}$

• B.

  B. $\large\dfrac{\sqrt{5}}{10}$

• C.

  C. $\large\dfrac{\sqrt{3}}{5}$

• D.

  D. $\large\dfrac{\sqrt{3}}{3}$

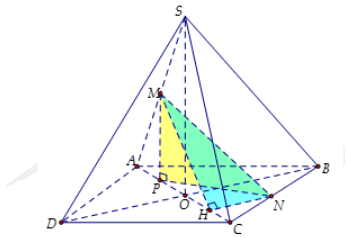
Do $\large S.ABCD$ là hình chóp đều nên ta có $\large SO\perp (ABCD)$.

Gọi $\large P$ là trung điểm của $\large AO$.

Khi đó $\large MP//SO\Rightarrow MP\perp (ABCD)$

Suy ra $\large\left ( \widehat{MN,(ABCD)} \right )=\widehat{MNP}=60^{\circ}$

Xét tam giác $\large NCP$, ta có:

$\large PN^{2}=CN^{2}+CP^{2}-2CN.CP.\cos 45^{\circ}=\frac{5a^{2}}{8}\Rightarrow PN=\dfrac{a\sqrt{10}}{4}$

Trong tam giác vuông $\large MNP$, ta có:

$\large \left\{\begin{align}MN=\dfrac{PN}{\cos \widehat{MNP}}=\dfrac{\dfrac{a\sqrt{10}}{4}}{\cos 60^{\circ}}=\dfrac{a\sqrt{10}}{2}\\ PM=NP\tan \widehat{MNP}=\dfrac{a\sqrt{30}}{4}\Rightarrow SO=2PM=\dfrac{a\sqrt{30}}{2}\end{align}\right.$

Gọi $\large H$ là trung điểm $\large OC$. Suy ra $\large NH//BD$ mà $\large BD\perp (SAC)\Rightarrow NH\perp (SAC)$

Do đó $\large \left ( \widehat{MN,(SAC))} \right )=\widehat{NMH}$

Ta có:

$\large NH=\dfrac{1}{2}OB=\dfrac{a\sqrt{2}}{4}\Rightarrow \sin \widehat{NMH}=\dfrac{NH}{MN}=\dfrac{a\sqrt{2}}{4}:\dfrac{a\sqrt{10}}{2}=\dfrac{\sqrt{5}}{10}$

Đáp án B