Cho hình chóp S.ABC có $\large SB=a, SC=2a, \widehat{BSC}=60^
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có SB=a,SC=2a,^BSC=60∘. Gọi M là chân đường cao kể từ đỉnh A của tam giác ABC và AM = 2a, góc tạo bởi SB và đáy ABC bằng 30∘. Tính khoảng cách h từ A đến mặt phẳng (SBC)
Đáp án án đúng là: B
Lời giải chi tiết:
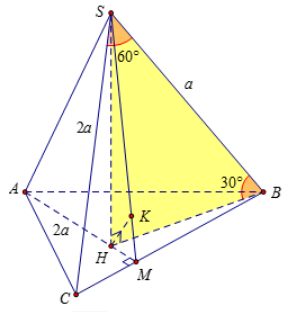
Do SH⊥(ABC)⇒(^SB,(ABC))=^SBH=30∘
Khi đó SH=SB⋅sin^SBH=a⋅sin30∘=a2
Áp dụng định lí cosin trong tam giác SBC ta có BC2=SB2+SC2−2SB.SC.cos60∘=5a2−2a2=3a2
⇒BC=a√3
Suy ra SABC=12AM.BC=a2√3
Khi đó
VS.ABC=13SH.SABC=13⋅a2⋅a2√3=a3√36
Mặt khác
SSBC=12SB.SC.sin^BSC=12a⋅2a⋅sin60∘=a2√32
Suy ra
h=d(A,(SBC))=3VS.ABCSSBC=3⋅a3√36a2√32=a
Đáp án B
Xem thêm các bài tiếp theo bên dưới