Cho hình chóp $\large S.ABCD$ có đáy là hình thoi tâm $\large O$, cạnh

Cho hình chóp $\large S.ABCD$ có đáy là hình thoi tâm $\large O$, cạnh bằng 1, $\large SO$ vuông góc với mặt đáy $\large (ABCD)$ và $\large SC=1$. Thể tích lớn nhất của khối chóp bằng:

• A.

  A. $\large\dfrac{2\sqrt{3}}{3}$

• B.

  B. $\large\dfrac{2\sqrt{3}}{9}$

• C.

  C. $\large\dfrac{2\sqrt{3}}{27}$

• D.

  D. $\large\dfrac{4\sqrt{3}}{27}$

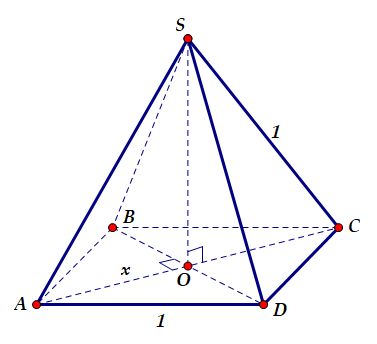
Đặt $\large OA=OC=x$. Suy ra $\large OD=\sqrt{1-x^{2}}$, $\large SO=\sqrt{1-x^{2}}$.

Điều kiện: $\large 0

Thể tích khối chóp

$\large V_{S.ABCD}=\dfrac{1}{3}S_{ABCD}.SO=\dfrac{1}{3}\cdot 2x\sqrt{1-x^{2}}\cdot \sqrt{1-x^{2}}=\dfrac{2}{3}x(1-x^{2})$
Xét hàm $\large f(x)=x(1-x^{2})$ trên $\large (0,1)$, ta được 

$\large\underset{(0,1)}{max}f(x)=f\left ( \dfrac{1}{\sqrt{3}} \right )=\dfrac{2}{3\sqrt{3}}$

Vậy thể tích lớn nhất của khối chóp bằng $\large\dfrac{4\sqrt{3}}{27}$

Đáp án D