Từ một mảnh giấy hình vuông cạnh $\large a$, người ta gấp thành hình l

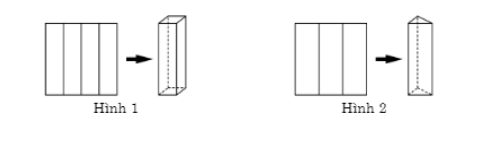
Từ một mảnh giấy hình vuông cạnh $\large a$, người ta gấp thành hình lăng trụ theo hai cách sau:

Cách 1: Gấp thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều có thể tích là $\large V_{1}$ (Hình 1)

Cách 2: Gấp thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều có thể tích $\large V_{2}$ (Hình 2)

Tính tỉ số $\large k=\frac{V_{1}}{V_{2}}$

• A.

  A. $\large k=\dfrac{3\sqrt{3}}{2}$

• B.

  B. $\large k=\dfrac{3\sqrt{3}}{4}$

• C.

  C. $\large k=\dfrac{3\sqrt{3}}{8}$

• D.

  D. $\large k=\dfrac{4\sqrt{3}}{9}$

Gọi cạnh hình vuông là $\large a$.

Suy ra cạnh đáy hình lăng trụ tứ giác là $\large\dfrac{a}{4}$, cạnh đáy hình lăng trụ tam giác là $\large\dfrac{a}{3}$

Khi đó $\large\dfrac{V_{1}}{V_{2}}=\dfrac{S_{1}h}{S_{2}h}=\dfrac{\left ( \dfrac{a}{4} \right )^{2}}{\left ( \dfrac{a}{3} \right )^{2}\cdot \dfrac{\sqrt{3}}{4}}=\dfrac{3\sqrt{3}}{4}$

Đáp án B